(本小题满分14分)已知数列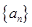 的各项均为正数,其前
的各项均为正数,其前 项和为
项和为 ,且满足
,且满足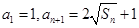 ,
,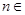 N
N .
.
(1)求 的值;
的值;
(2)求数列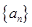 的通项公式;
的通项公式;
(3)是否存在正整数 , 使
, 使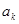 ,
, 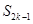 ,
, 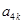 成等比数列? 若存在, 求
成等比数列? 若存在, 求 的值; 若不存在, 请说明理由.
的值; 若不存在, 请说明理由.
已知函数 ,
, .
.
(Ⅰ)若 与
与 在
在 处相切,试求
处相切,试求 的表达式;
的表达式;
(Ⅱ)若 在
在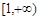 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;
(Ⅲ)证明不等式:

 .
.
四棱锥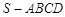 ,底面
,底面 为平行四边形,侧面
为平行四边形,侧面 底面
底面 .已知
.已知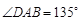 ,
,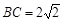 ,
,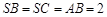 ,
,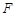 为线段
为线段 的中点.
的中点.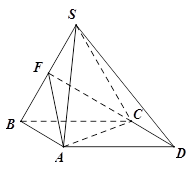
(Ⅰ)求证: 平面
平面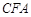 ;
;
(Ⅱ)求面 与面
与面 所成二面角大小.
所成二面角大小.
某学校的三个学生社团的人数分布如下表(每名学生只能参加一个社团):
| 围棋社 |
舞蹈社 |
拳击社 |
|
| 男生 |
5 |
10 |
28 |
| 女生 |
15 |
30 |
m |
学校要对这三个社团的活动效果进行抽样调查,按分层抽样的方法从三个社团成员中抽取18人,结果拳击社被抽出了6人.
(Ⅰ)求拳击社团被抽出的6人中有5人是男生的概率;
(Ⅱ)设拳击社团有X名女生被抽出,求X的分布列及数学期望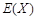 .
.
已知函数 ,记函数
,记函数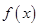 的最小正周期为
的最小正周期为 ,向量
,向量 ,
,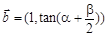 (
(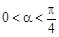 ),且
),且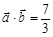 .
.
(Ⅰ)求 在区间
在区间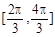 上的最值;
上的最值;
(Ⅱ)求 的值.
的值.
已知数列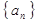 ,满足
,满足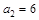 ,
,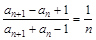
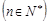 ,
,
(1)求 的值;
的值;
(2)猜想数列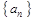 的通项公式
的通项公式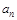 ,并用数学归纳法证明;
,并用数学归纳法证明;
(3)己知 ,设
,设 ,记
,记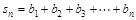 ,求
,求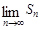 .
.