（本小题满分14分）已知椭圆
的中心在坐标原点，两焦点分别为双曲线
的顶点，直线
与椭圆交于
，
两点，且点的坐标为
，点
是椭圆上异于点,的任意一点，点
满足
，
，且，，三点不共线.
（1）求椭圆的方程；
（2）求点的轨迹方程；
（3）求
面积的最大值及此时点的坐标.
已知函数f(x)＝(x－1)2，g(x)＝4(x－1)，数列{an}是各项均不为0的等差数列，其前n项和为Sn，点(an＋1，S2n－1)在函数f(x)的图象上；数列{bn}满足b1＝2，bn≠1，且(bn－bn＋1)·g(bn)＝f(bn)(n∈N＋)．
(1)求an并证明数列{bn－1}是等比数列；
(2)若数列{cn}满足cn＝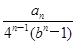
，证明：c1＋c2＋c3＋…＋cn<3.
正项数列{an}的前n项和Sn满足：
－(n2＋n－1)Sn－(n2＋n)＝0.
(1)求数列{an}的通项公式an；
(2)令bn＝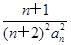
，数列{bn}的前n项和为Tn，证明：对于任意的n∈N*，都有Tn<
.
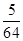已知数列{an}是首项为
，公比为的等比数列，设bn＋15log3an＝t，常数t∈N*.
(1)求证：{bn}为等差数列；
(2)设数列{cn}满足cn＝anbn，是否存在正整数k，使ck，ck＋1，ck＋2按某种次序排列后成等比数列？若存在，求k，t的值；若不存在，请说明理由．
在公差为d的等差数列{an}中，已知a1＝10，且a1,2a2＋2,5a3成等比数列．
(1)求d，an；
(2)若d<0，求|a1|＋|a2|＋…＋|an|.
已知公差不为零的等差数列{an}的前4项和为10，且a2，a3，a7成等比数列．
(1)求通项公式an；
(2)设bn＝2an，求数列{bn}的前n项和Sn.