(本小题满分10分)选修4-4:坐标系与参数方程
已知椭圆C: ,直线
,直线 (t为参数).
(t为参数).
(Ⅰ)写出椭圆C的参数方程及直线 的普通方程;
的普通方程;
(Ⅱ)设 ,若椭圆C上的点P满足到点A的距离与其到直线
,若椭圆C上的点P满足到点A的距离与其到直线 的距离相等,求点P的坐标.
的距离相等,求点P的坐标.
根据如图所示的程序框图,将输出的a,b值依次分别记为 其中
其中
(I)分别求数列 的通项公式;
的通项公式;
(II)令

(本小题满分12分)
已知数列 中,
中, (
( 为常数),
为常数),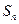 为
为 的前
的前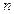 项和,且
项和,且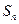 是
是 与
与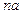 的等差中项.
的等差中项.
(Ⅰ)求 并归纳出
并归纳出 (不用证明);
(不用证明);
(Ⅱ)若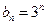 且
且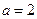 ,求数列
,求数列 的前
的前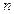 项和
项和 .
.
(本小题满分12分)
用黄、蓝、白三种颜色粉刷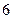 间办公室
间办公室
(Ⅰ) 若每间办公室刷什么颜色不要求,有多少种不同的粉刷方法?
(Ⅱ)若一种颜色粉刷 间,一种颜色粉刷
间,一种颜色粉刷 间,一种颜色粉刷
间,一种颜色粉刷 间,有多少种不同的粉刷方法?
间,有多少种不同的粉刷方法?
(Ⅲ)若每种颜色至少用一次,粉刷这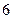 间办公室,有多少种不同的粉刷方法?
间办公室,有多少种不同的粉刷方法?
解:
(本小题满分12分)
在数列 中,已知
中,已知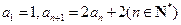
 (Ⅰ)求证:数列
(Ⅰ)求证:数列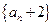 是等比数列;
是等比数列;
(Ⅱ) 求数列 的前
的前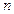 项和
项和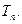
(本小题满分12分)
数列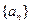 是首项
是首项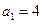 的等比
的等比 数列,且
数列,且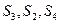 成等差数列.
成等差数列.
(Ⅰ)求数列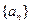 的通项公式;
的通项公式;
(Ⅱ)设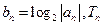 为数列
为数列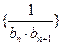 的前
的前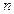 项和,求
项和,求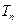 .
.