如图,椭圆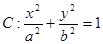
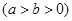 的顶点为
的顶点为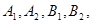 焦点为
焦点为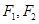 ,
,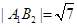 ,
,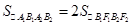 .
.
(1)求椭圆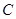 的方程;
的方程;
(2)设直线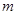 过
过 ,且与椭圆相交于
,且与椭圆相交于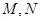 两点,当
两点,当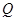 是
是 的中点时,求直线
的中点时,求直线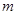 的方程.
的方程.
(3)设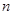 为过原点的直线,
为过原点的直线, 是与
是与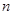 垂直相交于
垂直相交于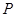 点且与椭圆相交于两点
点且与椭圆相交于两点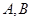 的直线,
的直线,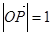 ,是否存在上述直线使以
,是否存在上述直线使以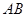 为直径的圆过原点?若存在,求出直线
为直径的圆过原点?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
已知A,B,C是椭圆W: +y2=1上的三个点,O是坐标原点.
+y2=1上的三个点,O是坐标原点.
(1)当点B是W的右顶点,且四边形OABC为菱形时,求此菱形的面积;
(2)当点B不是W的顶点时,判断四边形OABC是否可能为菱形,并说明理由.
每年的3月12日,是中国的植树节.林管部门在植树前,为保证树苗的质量,都会在植树前对树苗进行检测.现从甲、乙两种树苗中各抽测了10株树苗的高度,规定高于128厘米的树苗为“良种树苗”,测得高度如下(单位:厘米):
甲:137,121,131,120,129,119,132,123,125,133;
乙:110,130,147,127,146,114,126,110,144,146.
(1)根据抽测结果,画出甲、乙两种树苗高度的茎叶图,并根据你填写的茎叶图,对甲、乙两种树苗的高度作比较,写出对两种树苗高度的统计结论;
(2)设抽测的10株甲种树苗高度平均值为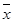 ,将这10株树苗的高度依次输入按程序框图进行运算(如图),问输出的S大小为多少?并说明S的统计学意义;
,将这10株树苗的高度依次输入按程序框图进行运算(如图),问输出的S大小为多少?并说明S的统计学意义;
(3)若小王在甲种树苗中随机领取了5株进行种植,用样本的频率分布估计总体分布,求小王领取到的“良种树苗”的株数X的分布列.
已知复数z1满足(z1-2)(1+i)=1-i(i为虚数单位),复数z2的虚部为2,且z1·z2是实数,求z2.
为了调查某大学学生在某天上网的时间,随机对100名男生和100名女生进行了不记名的问卷调查.得到了如下的统计结果:
表1:男生上网时间与频数分布表
| 上网时间(分钟) |
[30,40) |
[40,50) |
[50,60) |
[60,70) |
[70,80] |
| 人数 |
5 |
25 |
30 |
25 |
15 |
表2:女生上网时间与频数分布表
| 上网时间(分钟) |
[30,40) |
[40,50) |
[50,60) |
[60,70) |
[70,80] |
| 人数 |
10 |
20 |
40 |
20 |
10 |
(1)从这100名男生中任意选出3人,求其中恰有1人上网时间少于60分钟的概率;
(2)完成下面的2×2列联表,并回答能否有90%的把握认为“大学生上网时间与性别有关”?
| 上网时间少于60分钟 |
上网时间不少于60分钟 |
合计 |
|
| 男生 |
|||
| 女生 |
|||
| 合计 |
附:K2=
| P(K2≥k0) |
0.100 |
0.050 |
0.025 |
0.010 |
0.005 |
| k0 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
假设每天从甲地去乙地的旅客人数X是服从正态分布N(800,502)的随机变量.记一天中从甲地去乙地的旅客人数不超过900的概率为p0.
(1)求p0的值;(参考数据:若X~N(μ,σ2),有P(μ-σ<X≤μ+σ)=0.682 6,P(μ-2σ<X≤μ+2σ)=0.954 4,P(μ-3σ<X≤μ+3σ)=0.997 4)
(2)某客运公司用A、B两种型号的车辆承担甲、乙两地间的长途客运业务,每车每天往返一次.A、B两种车辆的载客量分别为36人和60人,从甲地去乙地的营运成本分别为1 600元/辆和2 400元/辆.公司拟组建一个不超过21辆车的客运车队,并要求B型车不多于A型车7辆.若每天要以不小于p0的概率运完从甲地去乙地的旅客,且使公司从甲地去乙地的营运成本最小,那么应配备A型车、B型车各多少辆?