在直角坐标系xOy中,椭圆C1: ="1" (a＞b＞0)的左、右焦点分别为F1、F2.F2也是抛物线C2：y2=4x的焦点，点M为C1与C2在第一象限的交点，且|MF2|=.（1）求C1的方程；（2）平面上的点N满足=+，直线l∥MN，且与C1交于A、B两点，若·=0，求直线l的方程.
(13分)已知函数，命题在区间上的最小值为命题方程的两根满足若命题与命题中有且只有一个真命题，求实数的取值范围.
．(13分)已知集合， （1）当时，求； （2）若，求实数的取值范围．
(13分)已知 (1)求的值； (2)求的值.
.数列满足：，且 （1）设，证明数列是等差数列；（2）求数列、的通项公式； （3）设，为数列的前项和，证明.
已知圆C:. (1)直线过点P(1,2)，且与圆C交于A、B两点，若，求直线的方程； (2)过圆C上一动点M作平行于y轴的直线m，设直线m与x轴的交点为N，若向量，求动点的轨迹方程； (3) 若点R(1,0)，在（2）的条件下，求的最小值及相应的点坐标.
试卷网 试题网 古诗词网 作文网 范文网
Copyright ©2020-2025 优题课 youtike.com 版权所有
粤ICP备20024846号
="1" (a＞b＞0)的左、右焦点分别为F1、F2.F2也是抛物线C2：y2=4x的焦点，点M为C1与C2在第一象限的交点，且|MF2|=
.
=
+
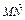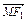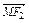，直线l∥MN，且与C1交于A、B两点，若
·
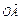=0，求直线l的方程.
，命题
在区间
上的最小值为
命题
方程
的两根
满足
若命题
与命题
中有且只有一个真命题，求实数
的取值范围.
，
时，求
；
，求实数
的取值范围．
的值；
的值.
满足：
，且
，证明数列
是等差数列；（2）求数列
，
为数列
的前
项和，证明
.
.
过点P(1,2)，且与圆C交于A、B两点，若
，求直线
，求动点
的轨迹方程；
的最小值及相应的