为了解心肺疾病是否与年龄相关,现随机抽取了40名市民,得到数据如下表:
| |
患心肺疾病 |
不患心肺疾病 |
合计 |
| 大于40岁 |
16 |
|
|
| 小于等于40岁 |
|
12 |
|
| 合计 |
|
|
40 |
已知在全部的40人中随机抽取1人,抽到不患心肺疾病的概率为
(1)请将 列联表补充完整;
列联表补充完整;
(2)已知大于40岁患心肺疾病市民中,经检查其中有4名重症患者,专家建议重症患者住院治疗,现从这16名患者中选出两名,记需住院治疗的人数为 ,求
,求 的分布列和数学期望;
的分布列和数学期望;
(3)能否在犯错误的概率不超过0.01的前提下认为患心肺疾病与年龄有关?
下面的临界值表供参考:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: ,其中
,其中 )
)
如图所示, 是⊙
是⊙ 直径,弦
直径,弦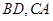 的延长线交于
的延长线交于 ,
,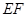 垂直于
垂直于 的延长线于
的延长线于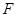 .求证:
.求证:
(1)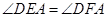 ;
;
(2)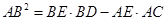 .
.
设函数 (
( ),其导函数为
),其导函数为 .
.
(1)当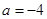 时,求
时,求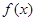 的单调区间;
的单调区间;
(2)当 时,
时,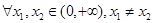 ,求证:
,求证: .
.
设 分别是椭圆
分别是椭圆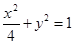 的左,右焦点.
的左,右焦点.
(1)若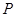 是椭圆在第一象限上一点,且
是椭圆在第一象限上一点,且 ,求
,求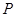 点坐标;
点坐标;
(2)设过定点 的直线
的直线 与椭圆交于不同两点
与椭圆交于不同两点 ,且
,且 为锐角(其中
为锐角(其中 为原点),求直线
为原点),求直线 的斜率
的斜率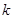 的取值范围.
的取值范围.
甲、乙两人参加某电视台举办的答题闯关游戏,按照规则,甲先从6道备选题中一次任意抽取3道题,独立作答,然后由乙回答剩余3题,每人答对其中的2题就停止答题,即闯关成功。已知6道备选题中,甲能答对其中的4道题,乙答对每道题的概率都是 .
.
(1)求甲、乙至少有一人闯关成功的概率;
(2)设甲答对题目的个数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
如图,已知三棱柱 的侧棱与底面垂直,且
的侧棱与底面垂直,且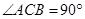 ,
, ,
,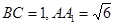 ,点
,点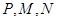 分别为
分别为 、
、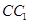 、
、 的中点.
的中点.
(1)求证: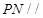 平面
平面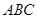 ;
;
(2)求证: ;
;
(3)求二面角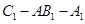 的余弦值.
的余弦值.