(本小题满分12分)如图,四棱锥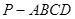 中,
中,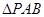 是正三角形,四边形
是正三角形,四边形 是矩形,且面
是矩形,且面 面
面 ,
, ,
, .
.
(Ⅰ)若点 是
是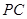 的中点,求证:
的中点,求证: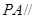 面
面 ;
;
(Ⅱ)若点 在线段
在线段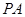 上,且
上,且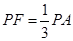 ,求三棱锥
,求三棱锥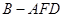 的体积.
的体积.
(本小题满分12分)在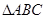 中,已知
中,已知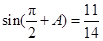 ,
, .
.
(1)求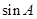 与
与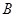 的值;
的值;
(2)若角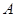 ,
,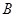 ,
,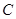 的对边分别为
的对边分别为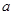 ,
,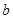 ,
,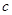 ,且
,且 ,求
,求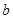 ,
,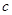 的值.
的值.
(本小题满分12分)将一枚骰子先后抛掷两次,观察向上的点数,
(1)求点数之和是5的概率;
(2)设a,b分别是将一枚骰子先后抛掷两次向上的点数,求等式 成立的概率。
成立的概率。
(本小题满分14分)已知椭圆 :
: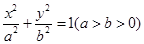 的上顶点为
的上顶点为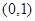 ,且离心率为
,且离心率为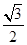 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)证明:过椭圆 :
: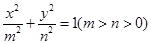 上一点
上一点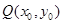 的切线方程为
的切线方程为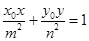 ;
;
(Ⅲ)从圆 上一点
上一点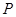 向椭圆
向椭圆 引两条切线,切点分别为
引两条切线,切点分别为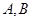 ,当直线
,当直线 分别与
分别与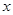 轴、
轴、 轴交于
轴交于 、
、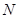 两点时,求
两点时,求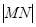 的最小值.
的最小值.
(本小题满分12分)如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB= ,PD⊥平面ABCD,PD=AD=1,点
,PD⊥平面ABCD,PD=AD=1,点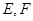 分别为AB和PD中点.
分别为AB和PD中点.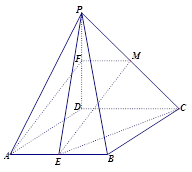
(Ⅰ)求证:直线AF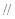 平面PEC ;
平面PEC ;
(Ⅱ)求PC与平面PAB所成角的正弦值.