(本小题满分12分)已知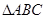 的内角
的内角 、
、 、
、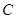 的对边分别为
的对边分别为 、
、 、
、 ,
,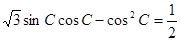 ,且
,且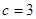
(1)求角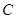 ;
;
(2)若向量 与
与 共线,求
共线,求 、
、 的值.
的值.
已知函数
(1)求函数 的最小正周期和图象的对称轴方程
的最小正周期和图象的对称轴方程
(2)求函数 在区间
在区间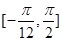 上的值域
上的值域
在直角坐标系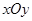 中,曲线
中,曲线 的参数方程为
的参数方程为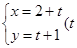 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点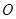 为极点,
为极点,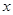 轴的正半轴为极轴的极坐标系下,曲线
轴的正半轴为极轴的极坐标系下,曲线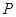 的方程为
的方程为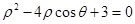 .
.
(1)求曲线 的普通方程和曲线
的普通方程和曲线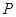 的直角坐标方程;
的直角坐标方程;
(2)设曲线 和曲线
和曲线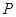 的交点为
的交点为 、
、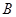 ,求
,求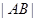 .
.
已知,椭圆C过点 ,两个焦点为
,两个焦点为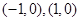 .
.
(1)求椭圆C的方程;
(2)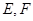 是椭圆C上的两个动点,如果直线
是椭圆C上的两个动点,如果直线 的斜率与
的斜率与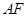 的斜率互为相反数,证明直线
的斜率互为相反数,证明直线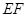 的斜率为定值,并求出这个定值.
的斜率为定值,并求出这个定值.
已知函数 .
.
(1)当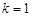 时,求函数
时,求函数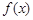 的最大值;
的最大值;
(2)若函数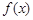 没有零点,求实数
没有零点,求实数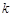 的取值范围;
的取值范围;
已知斜三棱柱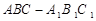 的底面是直角三角形,
的底面是直角三角形, 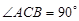 ,侧棱与底面所成角为
,侧棱与底面所成角为 ,点
,点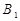 在底面上的射影
在底面上的射影 落在
落在 上.
上.
(1)求证: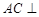 平面
平面 ;
;
(2)若 ,且当
,且当 时,求二面角
时,求二面角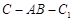 的大小.
的大小.