(本小题满分10分)设不等式 的解集为集合
的解集为集合 ,关于
,关于 的不等式
的不等式 的解集为集合
的解集为集合 .
.
(1)若 ,求实数
,求实数 的取值范围;
的取值范围;
(2)若 ∩
∩ ,求实数
,求实数 的取值范围.
的取值范围.
定义在 上的函数
上的函数 ,如果满足:对任意
,如果满足:对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 是
是 上的有界函数,其中
上的有界函数,其中 称为函数
称为函数 的上界.已知函数
的上界.已知函数 ,
,
(1)当 时,求函数
时,求函数 在
在 上的值域,并判断函数
上的值域,并判断函数 在
在 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数 在
在 上是以4为上界的有界函数,求实数
上是以4为上界的有界函数,求实数 的取值范围.
的取值范围.
已知向量 ,
, ,函数
,函数
(1)求 的单调递增区间;
的单调递增区间;
(2)若不等式 都成立,求实数m的最大值.
都成立,求实数m的最大值.
已知点 ,
,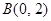 ,点
,点 在单位圆上.
在单位圆上.
(1)若 (
(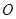 为坐标原点),求
为坐标原点),求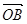 与
与 的夹角;
的夹角;
(2)若 ,求点
,求点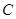 的坐标.
的坐标.
设全集为R,集合 ,
,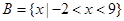 .
.
(1)求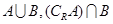 ;
;
(2)已知 ,若
,若 ,求实数
,求实数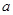 的取值范围.
的取值范围.