(10分)质量为m、带电荷量为+q的微粒在O点以初速度v0与水平方向成θ角射出,如图所示,重力加速度为g.
(1)如果微粒只在重力和电场力作用下沿v0方向做匀速直线运动,则电场的大小和方向。
(2)若微粒在运动过程中所受阻力的大小恒为f.如果在某方向上加上一定大小的匀强电场后,能保证微粒仍沿v0方向做直线运动,试求所加匀强电场电场强度的最小值.
在压强 ---温度
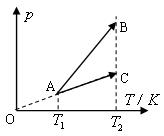
---温度 的坐标系中,一定质量的某种理想气体先后发生以下两种状态变化过程:第一种变化是从状态A到状态B,外界对该气体做功为
的坐标系中,一定质量的某种理想气体先后发生以下两种状态变化过程:第一种变化是从状态A到状态B,外界对该气体做功为 ;第二种变化是从状态A到状态C,该气体从外
;第二种变化是从状态A到状态C,该气体从外 界吸收热量为
界吸收热量为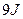 。图线AC反向延长线通过坐标原点O,B、C两状态的温度相同,理想气体的分子势能为零。求:
。图线AC反向延长线通过坐标原点O,B、C两状态的温度相同,理想气体的分子势能为零。求:
(1)从状态A到状态C过程,该气体对外界做功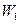 和其内能的增量
和其内能的增量 ;
;
(2)从状态A到状态B过程,该气体内能的增量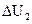 及其从外界吸收的热量
及其从外界吸收的热量 。
。
如图所示是一列沿x轴正方向 传播的简谐横波在t=0时刻的波形图,已知波的传播速度v=2m/s.试回答下列问题:
传播的简谐横波在t=0时刻的波形图,已知波的传播速度v=2m/s.试回答下列问题:
(1)该波的波长 为多大;
为多大;
(2)该波 的周期
的周期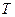 为多大;
为多大;
(3)写出 处质点的振动函数表达式;
处质点的振动函数表达式;
(4)求出 处质点在0~4.5s内通过的路程
处质点在0~4.5s内通过的路程 及t=4.5s时刻的位移
及t=4.5s时刻的位移 。
。
已知潜水员在岸上和海底吸入空气的密度分别为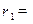 1.2kg/
1.2kg/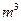 和
和 2.0kg/
2.0kg/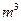 ,空气的摩尔质量
,空气的摩尔质量 0.029kg/mol,阿伏伽德
0.029kg/mol,阿伏伽德 罗常数
罗常数
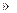 6.0
6.0 。若潜水员呼吸一次吸入
。若潜水员呼吸一次吸入 2L空气,试估算潜水员在海底比在岸上每呼吸一次多吸入空气的分子数
2L空气,试估算潜水员在海底比在岸上每呼吸一次多吸入空气的分子数 。(结果保留一位有效数字)
。(结果保留一位有效数字)
如图4-9所示,一个横截面为直角三角形的三棱镜,ÐA=30°,ÐC=90°.三棱镜材料的折射率是 n=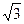 。一条与BC面成θ=30°角的光线射向BC面,经过AC边一次反射从AB边射出。
。一条与BC面成θ=30°角的光线射向BC面,经过AC边一次反射从AB边射出。
(1)求光在三棱镜中的速度
(2)画出此束光线通过棱镜的光路图
(3)求从AB边射出光线与AB边的夹角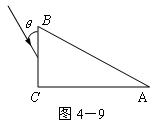
质量m为10g的子弹,以v=300m/s的速度射入质量M为50g静止在水平桌面上的木块,并留在木块中。
(1)当子弹留在木块中以后,木块运动的速度v1是多大?
(2)如果子弹把木块打穿,子弹穿过后的速度v'为100m/s,这时木块的速度v2又是多大?