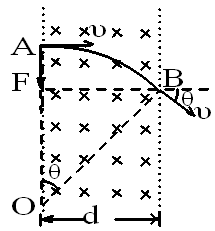
如图所示，在光滑水平地面上有一质量为2m的长木板，其左端放有一质量为m的重物（可视为质点），重物与长木板之间的动摩擦因数为。开始时，长木板和重物都静止，现在给重物一初速度v0，已知长木板撞到前方固定的障碍物时，长木板和重物的速度恰好相等，长木板与障碍物发生碰撞时不损失机械能，重物始终不从长木板上掉下来。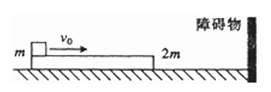
（1）求长木板与前方固定的障碍物相撞时的速度的大小；
（2）求长木板撞到前方固定的障碍物前运动的位移大小；
（3）求重物最终在长木板上相对滑动的距离大小。
如图所示，固定于水平桌面上的金属框架cdef，处在竖直向下的匀强磁场中，金属棒ab搁在框架上，可无摩擦滑动。此时abed构成一个边长为l的正方形，棒ab的电阻为r，其余部分电阻不计，开始时磁感应强度为B0。
⑴若
从t=0时刻起，磁感应强度均匀增加，每秒增加量为k，同时保持棒静止，求棒中的感应电流，并在图上标出电流方向；
⑵在上述⑴情况下，始终保持棒静止，当t=t1时需施加垂直于棒的水平拉力多大？
⑶若从t=0时刻起，磁感应强度逐渐减小，当棒以恒定的速度v向右匀速运动时，可使棒中不产生感应电流，则磁感应强度怎样随时间变化（
写出B与t的关系式）？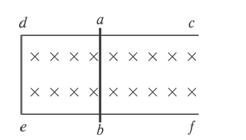
一辆值勤的警车停在公路边，当警员发现从他旁边以10m/s的速度匀速行驶的货车严重超载时，决定前去追赶，
经过2.5s后警车发动起来，并以2.5m/s2的加速度做匀加速运动。问：
⑴警车在追赶货车的过程中，两车间的最大距离是多少？
⑵警车发动后要多长时间才能追上货车？此时警车速度多大？
如图所示，在第一象限有一匀强电场，场强大小为E，方向与y轴平行；在x轴下方有一匀强磁场，磁场方向与纸面垂直。一质量为m、电荷量为－q（q＞0）的粒子以平行于x轴的速度从y轴上的P点处射入电场，在x轴上的Q点处进入磁场，并从坐标原点O离开磁场，粒子在磁场中的运动轨迹与y轴交于M点，已知OP＝L，OQ＝
L，不计重力，求：
（1）匀强电场和匀强磁场的方向。
（2）M点与坐标原点O之间的距离。
（3）粒子从P点运动到M点所用的时间。
已知质量为m的带电液滴，以速度v射入互相垂直的匀强电场E和匀强磁场B中，液滴在此空间刚好能在竖直平面内做匀速圆周运动，如图所示，求：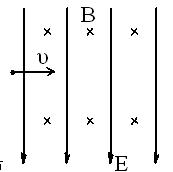
（1）液滴在空间受到几个力作用。
（2）液滴带电荷量及电性。
（3）液滴做匀速圆周运动的半径多大？
如图所示，一束电子的电荷量为e，以速度v垂直射入磁感应强度为B、宽度为d的有界匀强磁场中，穿过磁场时的速度方向与原来电子的入射方向的夹角θ是300,则电子的质量是多少？电子穿过磁场的时间又是多少？