如图,直线l1: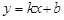 与x轴交于点B(1,0),直线l2:
与x轴交于点B(1,0),直线l2: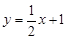 与y轴交于点C,这两条直线交于A(2,a).
与y轴交于点C,这两条直线交于A(2,a).
(1)直接写出a的值;
(2)求点C的坐标;
(3)求直线l1的表达式;
(4)求四边形ABOC的面积.
计算:
(本题满分10分,每小题5分)
请你把上面的解答再认真地检查一遍,别留下什么遗憾,并估算一下成绩是否达到了80分,如果你的全卷得分低于80分,则本题的得分将计入全卷总分,但计入后全卷总分最多不超过80分;如果你全卷得分已经达到或超过80分,则本题的得分不计入全卷总分.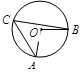
(1)计算 -2 +3的结果是_ _;
(2)如图,点C在⊙O上,∠ACB=50°,则∠AOB=_ _°
如图,将OA = 6,AB = 4的矩形OABC放置在平面直角坐标系中,动点M、N以每秒1个单位的速度分别从点A、C同时出发,其中点M沿AO向终点O运动,点N沿CB向终点B运动,当两个动点运动了t秒时,过点N作NP⊥BC,交OB于点P,连接MP.
(1)点B的坐标为 ;用含t的式子表示点P的坐标为;(3分)
(2)记△OMP的面积为S,求S与t的函数关系式(0 < t < 6);并求t为何值时,S有最大值?(4分)
(3)试探究:当S有最大值时,在y轴上是否存在点T,使直线MT把△ONC分割成三角形和四边形两部分,且三角形的面积是△ONC面积的 ?若存在,求出点T的坐标;若不存在,请说明理由.(3分)
?若存在,求出点T的坐标;若不存在,请说明理由.(3分)
(本题满分10分,每小题5分)
如图,AB为⊙O的直径,弦CD⊥AB,垂足为点M,AE切⊙O于点A,交BC的延长线于点E,连接AC.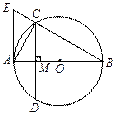
(1)若∠B=30°,AB=2,求CD的长;
(2)求证:AE2=EB·EC.
为了解某住宅区的家庭用水量情况,从该住宅区中随机抽样调查了50户家庭去年每个月的用水量,统计得到的数据绘制了下面的两幅统计图.图24-1是去年这50户家庭月总用水量的折线统计图,图24-2是去年这50户家庭月总用水量的不完整的频数分布直方图.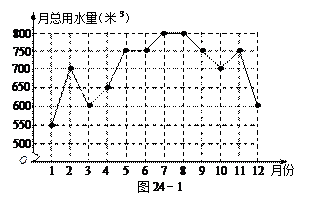

(1)根据图24-1提供的信息,补全图24-2中的频数分布直方图;(3分)
(2)在抽查的50户家庭去年月总用水量这12个数据中,极差是立方米,众数
是立方米,中位数是立方米;(3分)
(3)请你根据上述提供的统计数据,估计该住宅区今年每户家庭平均每月的用水量是多少立方米?(4分)