在某次测验中，有6位同学的平均成绩为75分，用
表示编号为
的同学所得成绩，且前5位同学的成绩如下：
编号 |
1 |
2 |
3 |
4 |
5 |
| 成绩 |
70 |
76 |
72 |
70 |
72 |
（1）求第6位同学的成绩
，及这6位同学成绩的标准差s；
（2）从前5位同学中，随机地选2位同学，求恰有1位同学成绩在区间（68，75）中的概率．
计算下列定积分的值：
（1）
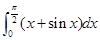；（2）
.
已知圆
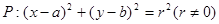满足：
①截y轴所得弦长为2；
②被x轴分成两段圆弧，其弧长的比为
.
求在满足条件①②的所有圆中，使代数式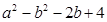
取得最小值时，圆的方程．
已知半径为5的圆的圆心在
轴上，圆心的横坐标是整数，且与直线
相切．
求：（1）求圆的方程；
（2）设直线
与圆相交于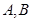
两点，求实数
的取值范围；
（3）在（2）的条件下，是否存在实数，使得过点
的直线
垂直平分弦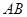
？
若存在，求出实数
的值；若不存在，请说明理由．
已知函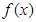数
对任意实数
恒有
且当
时，有
且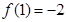
.
(1)判断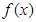的奇偶性；
(2)求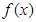在区间
上的最大值；
(3)解关于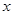
的不等式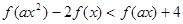
.
已知点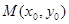
在圆
上运动，
，点
为线段MN的中点．
(1)求点的轨迹方程；
(2)求点到直线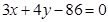
的距离的最大值和最小值．．