已知椭圆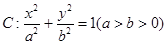 的离心率为
的离心率为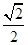 ,且过点
,且过点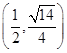 .
.
(1)求椭圆C的标准方程;
(2)设F是椭圆C的左焦点,过点P(-2,0)的直线交椭圆于A,B两点,求△ABF面积的最大值.
(本小题满分13分)
已知⊙C经过点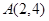 、
、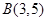 两点,且圆心C在直线
两点,且圆心C在直线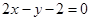 上.
上.
(1)求⊙C的方程;
(2)若直线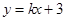 与⊙C总有公共点,求实数
与⊙C总有公共点,求实数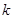 的取值范围.
的取值范围.
(本小题满分13分)
如图,在直三棱柱ABC-A1B1C1中,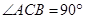 ,
,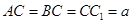 ,
,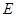 是
是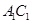 的中点,
的中点, 是
是 中点.
中点.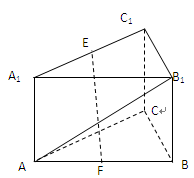
(1)求证: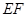 ∥面
∥面 ;
;
(2)求直线EF与直线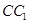 所成角的正切值;
所成角的正切值;
(3)设二面角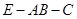 的平面角为
的平面角为 ,求
,求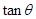 的值.
的值.
(本小题满分12分)
如图示,AB是圆柱的母线,BD是圆柱底面圆的直径,C是底面圆周上一点,E是AC中点,且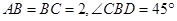 .
.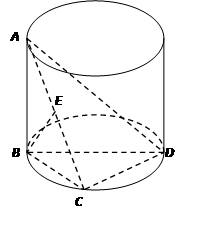
(1)求证: ;
;
(2)求直线BD与面ACD所成角的大小.
(本小题满分12分)
已知直线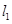 :
: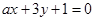 ,
, :
: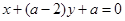 .
.
(1)若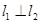 ,求实数
,求实数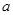 的值;
的值;
(2)当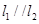 时,求直线
时,求直线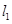 与
与 之间的距离.
之间的距离.
(本小题满分11分)
如图示,给出的是某几何体的三视图,其中正视图与侧视图都是边长为2的正三角形,俯视图为半径等于1的圆.试求这个几何体的侧面积与体积.