如图，将边长为4的正方形置于平面直角坐标系第一象限，使AB边落在x轴正半轴上，且A点的坐标是（1，0）．
（1）直线
经过点C，且与x轴交于点E，求四边形AECD的面积；
（2）若直线l经过点E，且将正方形ABCD分成面积相等的两部分，求直线l的解析式；
（3）若直线l1经过点F（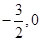
）且与直线y=3x平行．将（2）中直线l沿着y轴向上平移1个单位，交x轴于点M，交直线l1于点N，求△NMF的面积．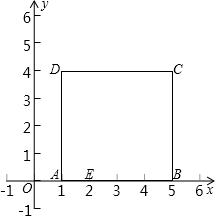
计算：
．
计算: （-1)2015+sin300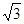+(2-
）(2+）．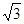
计算：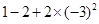
．
如图，在▱ABCD中，对角线AC、BD相交于点O，点E、F是AD上的点，且AE=EF=FD．连接BE、BF，使它们分别与AO相交于点G、H．
（1）求EG：BG的值；
（2）求证：AG=OG；
（3）设AG=a，GH=b，HO=c，求a：b：c的值．
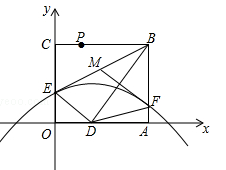
如图，折叠矩形OABC的一边BC，使点C落在OA边的点D处，已知折痕BE=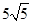
，且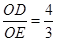
，以O为原点，OA所在的直线为x轴建立如图所示的平面直角坐标系，抛物线l：
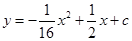经过点E，且与AB边相交于点F．
（1）求证：△ABD∽△ODE；
（2）若M是BE的中点，连接MF，求证：MF⊥BD；
（3）P是线段BC上一点，点Q在抛物线l上，且始终满足PD⊥DQ，在点P运动过程中，能否使得PD=DQ？若能，求出所有符合条件的Q点坐标；若不能，请说明理由．