（本题10分）如图，点C是线段AB的中点．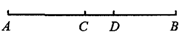
（1）若点D在线段CB上，且DB=3.5cm，AD=6.5cm，求线段CD的长度；
（2）若将（1）中的点“D在线段CB上”改为“点D在直线CB上”，其它条件不变，请画出相应的示意图，并求出此时线段CD的长度；
（3）若线段AB="12" cm，点C在AB上，点D、E分别是AC和BC的中点．
①当点C恰是AB中点时，则DE= cm．
②当AC=4cm,时，求DE的长；
③当点C在线段AB上运动时（点C与A、B重合除外），求DE的长．
如图11，正比例函数
的图像与一次函数
的图像交于点A(ｍ，2)， 一次函数图像经过点B
, 
与y轴的交点为C与
轴的交点为D．
（1）求一次函数解析式；
（2）求C点的坐标；
（3）求△AOD的面积。
（本小题满分9分）
作为一项惠农强农应对国际金融危机、拉动国内消费需求的重要措施，“家电下乡”工作已取得成效，在气温较低的季节，电冰箱也有一定的销量．我市某家电公司营销点对自去年10月份至今年3月份销售两种不同品牌冰箱
的数量做出统计，数据如图10所示： 
根据图10提供的信息解答下列问题：
（1）请你从平均数角度对这6个月甲、乙两品牌冰箱的销售量作出评价．
（2）请你从方差角度对这6个月甲、乙两品牌冰箱的销售情况作出评价．
（3）请你依据折线图的变化趋势，对营销点今后的进货情况提出建议．
如图9，
的半径为2，直径
经过弦
的中点
，∠ADC=75°．
（1）填空：
＝____________；
（2）求
的长．
(本小题满分8分)
先化简，再求值：
，其中
．
（1）认真观察，并在④后面的横线上写出相应的等式。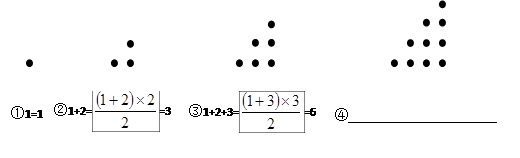
（2）【结合（1）观察下列点阵图，并在5后面的横线上写出相应的等式。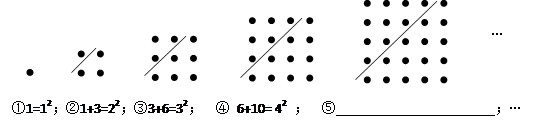
（3）通过猜想，写出（2）中与第n个点阵相对应的等式