（本题满分10分．为方便答题，可在答卷上画出你认为必要的图形）
如图，矩形ABCD中，AB=20，BC=10，点P为AB边上一动点，DP交AC于点Q．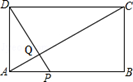
（1）求证：△APQ∽△CDQ；
（2）P点从A点出发沿AB边以每秒1个单位长度的速度向B点移动，移动时间为t秒．当t为何值时，DP⊥AC？
下列材料来自2006年5月衢州有关媒体的真实报道：有关部
门进行民众安全感满意度调查，方法是：在全市内采用等距抽样，抽取32个小区，共960户，每户抽一名年满16周岁并能清楚表达意见的人，同时，对比前一年的调查结果，得到统计图如下：
求：①写出2005年民众安全感满意度的众数选项是_______________；
②该统计表存在一个明显的错误是________________________；
③若记很安全，安全，基本安全，不安全，很不安全每项分值分别为100，80，60，40，0，请估计2005年该市民众安全感满意度的平均得分
先化简，再求值：
，其中a=﹣5．
已知抛物线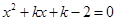
（1）求证：不论k为任何实数，抛物线与
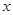轴总有两个交点；（2）若反比例函数
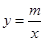的图象与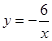
的图象关于y轴对称，又与抛物线交于点A(n,－3)，求抛物线的解析式；（3）若点P是(2)中抛物线上的一点，且点P到两坐标轴的距离相等，求点P的坐标.
已知抛物线C1：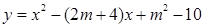
的顶点A到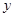
轴的距离为3， 与
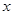轴交于C、D两点.（1）求顶点A的坐标；
（2）若点B在抛物线C1上，且
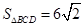，求点B的坐标.
如图，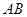
为⊙O的直径，
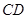是弦，且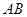
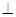
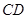于点E．连接
、
、
．
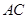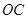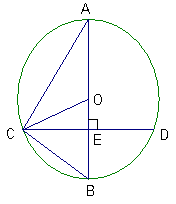
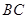（1）求证：
=
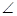
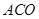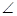
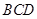． （2）若
=
，=
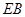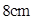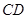，求⊙O的直径．