以平面直角坐标系的原点为极点，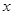
轴的正半轴为极轴，建立极坐标系，两种坐标系中取相同的长度单位，已知直线
的参数方程是
（
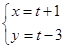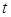为参数），圆
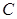的极坐标方程是
．
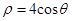（Ⅰ）求直线
的方程和圆
的直角坐标方程；
（Ⅱ）求直线被圆截得的弦长．
某观测站C在A城的南偏西20°的方向.由A城出发的一条公路，走向是南偏东40°，在C处测得公路上B处有一人距C为31千米正沿公路向A城走去，走了20千米后到达D处，此时CD间的距离为21千米，问这人还要走多少千米才能到达A城？
如图所示，已知半圆的直径AB=2，点C在AB
的延长线上，BC=1，点P为半圆上的一个动点，以
DC为边作等边△PCD，且点D与圆心O分别在PC
的两侧，求四边形OPDC面积的最大值.
沿一条小路前进，从A到B，方位角（从正北方向顺时针转到AB方向所成的角）是
50°，距离是3 km，从B到C，方位角是110°，距离是3 km，从C到D,方位角是140°，距离是（9+3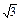
）km.试画出示意图，并计算出从A到D的方位角和距离（结果保留根号）.
在△ABC中，角A、B、C的对边分别为a、b、c，已知a+b=5，c=
，且4sin2
-cos2C=
.
(1)求角C的大小；
（2）求△ABC的面积.
已知a、b、c是△ABC的三边长，关于x的方程ax2-2
x-b="0" (a＞c＞b)的两根之差的平方等于4，△ABC的面积S=10
，c=7.
（1）求角C；
（2）求a，b的值.