已知曲线 的极坐标方程是
的极坐标方程是 ,直线
,直线 的参数方程是
的参数方程是 (
( 为参数).
为参数).
(Ⅰ)将曲线 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(Ⅱ)设直线 与
与 轴的交点是
轴的交点是 ,
, 是曲线
是曲线 上一动点,求
上一动点,求 的最大值.
的最大值.
(本小题8分)已知圆C:  及直
及直
(1)证明:不论m取何值,直线l与圆C恒相交;
(2)求直线l被圆C截得的弦长最短时的直线方程.
(本小题8分)已知线段AB的两个端点A、B分别在x轴和y轴上滑动,且∣AB∣=2.
(1)求线段AB的中点P的轨迹C的方程;
(2)求过点M(1,2)且和轨迹C相切的直线方程.
(本小题8分) 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,
若F,E分别为PC,BD的中点,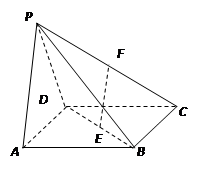
求证:
(l)EF∥平面PAD;
(2)平面PDC⊥平面PAD
设函数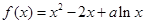 .
.
(1)若函数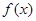 是定义域上的单调函数,求实数
是定义域上的单调函数,求实数 的取值范围;
的取值范围;
(2)求函数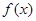 的极值点.
的极值点.
已知函数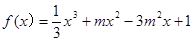
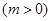 .
.
(1)若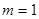 ,求曲线
,求曲线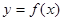 在点
在点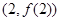 处的切线方程;
处的切线方程;
(2)若函数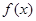 在区间
在区间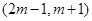 上单调递增,求实数
上单调递增,求实数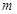 的取值范围.
的取值范围.