(本小题满分16分)已知数列 是以
是以 为公差的等差数列,数列
为公差的等差数列,数列 是以
是以 为公比的等比数列.(Ⅰ)若数列
为公比的等比数列.(Ⅰ)若数列 的前
的前 项和为
项和为 ,且
,且 ,
, ,求整数
,求整数 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,试问数列 中是否存在一项
中是否存在一项 ,使得
,使得 恰好可以表示为该数列中连续
恰好可以表示为该数列中连续 项的和?请说明理由;(Ⅲ)若
项的和?请说明理由;(Ⅲ)若 (其中
(其中 ,且(
,且( )是(
)是( )的约数),求证:数列
)的约数),求证:数列 中每一项都是数列
中每一项都是数列 中的项.
中的项.
(1)求数列 的通项公式
的通项公式
(2)求数列 的前n项和
的前n项和
已知a= ,c=2,B=150°,求边b的长及
,c=2,B=150°,求边b的长及
设函数 是定义在
是定义在 上的减函数,并且满足
上的减函数,并且满足 ,
,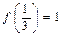 ,
,
(1)求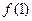 ,
,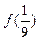 ,
, 的值, (2)如果
的值, (2)如果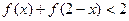 ,求x的取值范围。
,求x的取值范围。
(满分12分) 某商店按每件80元的价格,购进商品1000件(卖不出去的商品将成为废品);市场调研推知:当每件售价为100元时,恰好全部售完;当售价每提高1元时,销售量就减少5件;为获得最大利润,商店决定提高售价 元,获得总利润
元,获得总利润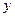 元.
元.
(1)请将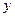 表示为
表示为 的函数;
的函数;
(2)当售价为多少时,总利润取最大值,并求出此时的利润.
函数 是R上的偶函数,且当
是R上的偶函数,且当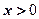 时,函数的解析式为
时,函数的解析式为
(1)求 的值;
的值;
(2)用定义证明 在
在 上是减函数;
上是减函数;
(3)求当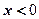 时,函数的解析式;
时,函数的解析式;