如图,三棱柱ABC-A B
B C
C 的侧面A
的侧面A ACC
ACC 与底面ABC垂直,AB=BC=CA=4,且AA
与底面ABC垂直,AB=BC=CA=4,且AA ⊥A
⊥A C,AA
C,AA =A
=A C.
C.
(Ⅰ)证明:AC⊥BA ;
;
(Ⅱ)求侧面A ABB
ABB 与底面ABC所成二面角的余弦值.
与底面ABC所成二面角的余弦值.
在某国际高端经济论坛上,前六位发言的是与会的含有甲、乙的6名中国经济学专家,他们的发言顺序通过随机抽签方式决定.
(Ⅰ)求甲、乙两位专家恰好排在前两位出场的概率;
(Ⅱ)发言中甲、乙两位专家之间的中国专家数记为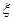 ,求
,求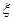 的分布列和数学期望.
的分布列和数学期望.
已知函数 在
在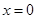 处取得极值.
处取得极值.
(1)求实数 的值;
的值;
(2)若关于 的方程
的方程 在区间
在区间 上恰有两个不同的实数根,求实数
上恰有两个不同的实数根,求实数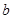 的取值范围;
的取值范围;
(3)证明:对任意的正整数 ,不等式
,不等式 都成立.
都成立.
已知椭圆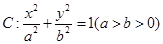 的离心率为
的离心率为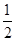 ,直线
,直线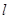 过点
过点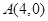 ,
, ,且与椭圆
,且与椭圆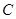 相切于点
相切于点 .(Ⅰ)求椭圆
.(Ⅰ)求椭圆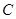 的方程;(Ⅱ)是否存在过点
的方程;(Ⅱ)是否存在过点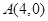 的直线
的直线 与椭圆
与椭圆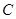 相交于不同的两点
相交于不同的两点 、
、 ,使得
,使得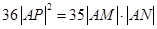 ?若存在,试求出直线
?若存在,试求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
设数列 的前
的前 项和为
项和为 .已知
.已知 ,
, ,
,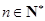 .
.
(Ⅰ)求数列 的通项公式;(Ⅱ)记
的通项公式;(Ⅱ)记 为数列
为数列 的前
的前 项和,求
项和,求 .
.