在某国际高端经济论坛上,前六位发言的是与会的含有甲、乙的6名中国经济学专家,他们的发言顺序通过随机抽签方式决定.
(Ⅰ)求甲、乙两位专家恰好排在前两位出场的概率;
(Ⅱ)发言中甲、乙两位专家之间的中国专家数记为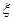 ,求
,求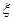 的分布列和数学期望.
的分布列和数学期望.
设数列 的前
的前 项和为
项和为 ,且
,且 ,
, .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
已知函数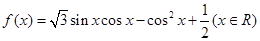 .
.
(1)求函数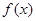 的最小正周期;
的最小正周期;
(2)求函数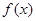 在区间
在区间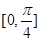 上的函数值的取值范围.
上的函数值的取值范围.
已知椭圆 过点
过点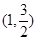 ,且离心率
,且离心率 。
。
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)若直线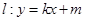 与椭圆
与椭圆 相交于
相交于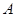 ,
,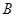 两点(
两点( 不是左右顶点),椭圆的右顶点为D,且满足
不是左右顶点),椭圆的右顶点为D,且满足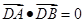 ,试判断直线
,试判断直线 是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由。
是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由。
已知函数 .
.
(I)求函数 的单调递减区间;
的单调递减区间;
(II)若 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围;
(III)过点 作函数
作函数 图像的切线,求切线方程
图像的切线,求切线方程
设数列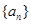 的前n项和为
的前n项和为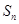 ,已知
,已知 ,
,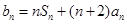 ,数列
,数列 是公差为d的等差数列,
是公差为d的等差数列,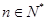 .
.
(1)求d的值;
(2)求数列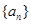 的通项公式;
的通项公式;
(3)求证: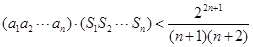 .
.