关于
的不等式
．
（Ⅰ）当
时，解此不等式；
（Ⅱ）设函数
，当
为何值时，
恒成立？
（本小题满分13分）某工厂对一批产品的质量进行了抽样检测，右图是根据抽样检测后的产品净重（单位：克）数据绘制的频率分布直方图.已知样本中产品净重小于100克的个数是36个。
（I）求样本中净重在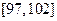
（克）的产品个数；
（II）若规定净重在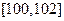
（克）的产品为一等品，依此抽样数据，求从该工厂随机抽取的3个产品中一等品个数
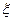的分布列和数学期望.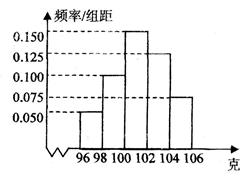
（本小题满分10分）选修4—5：不等式选讲
已知：a、b、x、y∈R+，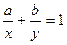
， 求证：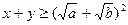
（（本小题满分10分）选修4—4：作标系与参数方程
（1）已知点C 的极坐标为（2，
），画图并求出以C为圆心，半径r=2的圆的极坐标
方程（写出解题过程）；
（2）P是以原点为圆心，r=2的圆上的任意一点，Q（6，0），M是PQ中点
①画图并写出⊙O的参数方程；
②当点P在圆上运动时，求点M的轨迹的参数方程。
22．（本小题满分10分）选修4—1：几何证明选讲
如图所示，AB为⊙O的直径，BC、CD为⊙O′的切线，B、D为切点
（1）求证：AD∥OC；
（2）若⊙O的半径为1，求AD·OC的值.
（（本小题满分12分）
若函数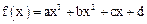
是奇函数，且
。
（1）求函数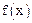
的解析式；
（2）求函数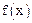在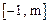
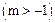上的最大值；
（3）设函数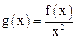
，若不等式
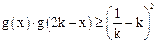在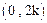
上恒成立，求实数k的取值范围．