(本小题满分为14分) 如图,过四棱柱 形木块上底面内的一点
形木块上底面内的一点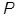 和下底面的对角线
和下底面的对角线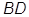 将木块锯开,得到截面
将木块锯开,得到截面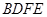 .
.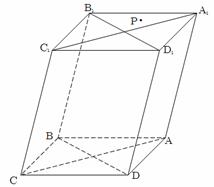
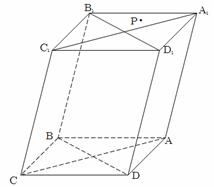
(1)请在木块的上表面作出过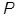 的锯线
的锯线 ,并说明理由;
,并说明理由;
(2)若该四棱柱的底面为菱形,四边形 是矩形时,试证明:平面
是矩形时,试证明:平面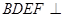 平面
平面 .
.
(本小题满分12分)
广州某商场根据以往某种商品的销售记录,绘制了日销售量的频率分布表(如表)和频率分布直方图(如图).
| 分组 |
频数 |
频率 |
 |
 |
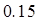 |
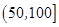 |
 |
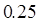 |
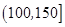 |
 |
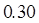 |
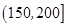 |
 |
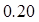 |
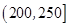 |
 |
 |

将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
(1)求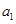 ,
,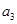 的值.
的值.
(2)求在未来连续3天里,有连续2天的日销售量都高于100个且另1天的日销售量不高于50
个的概率;
(3)用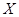 表示在未来3天里日销售量高于100个的天数,求随机变量
表示在未来3天里日销售量高于100个的天数,求随机变量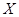 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)
已知函数
 R
R ,
,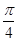 是函数
是函数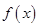 的一个零点.
的一个零点.
(1)求 的值,并求函数
的值,并求函数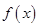 的单调递增区间;
的单调递增区间;
(2)若
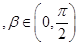 ,且
,且 ,
, ,求
,求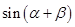 的值.
的值.
(本题14分)张老师居住在某城镇的A处,准备开车到学校B处上班。若该地各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图。(例如:A→C→D算作两个路段:路段AC发生堵车事件的概率为 ,路段CD发生堵车事件的概率为
,路段CD发生堵车事件的概率为 )。(1)请你为其选择一条由A到B的路线,使得途中发生堵车事件的概率最小;(2)若记路线A→C→F→B中遇到堵车次数为随机变量
)。(1)请你为其选择一条由A到B的路线,使得途中发生堵车事件的概率最小;(2)若记路线A→C→F→B中遇到堵车次数为随机变量 ,求
,求 的数学期望
的数学期望 。
。
(本题12分) 某县教研室要分析学生初中升学的数学成绩对高一年级数学成绩有什么影响,在高一年级学生中随机抽选10名学生,分析他们入学的数学成绩和高一年级期末数学考试成绩(如下表):
| 学生编号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 入学成绩x |
63 |
67 |
45 |
88 |
81 |
71 |
52 |
99 |
58 |
76 |
| 高一期末成绩y |
65 |
78 |
52 |
82 |
92 |
89 |
73 |
98 |
56 |
75 |
(1)计算入学成绩 与高一期末成绩
与高一期末成绩 的相关系数;
的相关系数;
(2)对变量 与
与 进行相关性检验,如果
进行相关性检验,如果 与
与 之间具有线性相关关系,求出线性回归方程;(3)若某学生入学数学成绩是80分,试估测他高一期末数学考试成绩。
之间具有线性相关关系,求出线性回归方程;(3)若某学生入学数学成绩是80分,试估测他高一期末数学考试成绩。
(本题12分) 甲箱的产品中有5个正品和3个次品,乙箱的产品中有4个正品和3个次品。
(1)从甲箱中任取2个产品,求这2个产品都是次品的概率;
(2)若从甲箱中任取2个产品放入乙箱中,然后再从乙箱中任取一个产品,求取出的这个产品是正品的概率。