（本小题满分15分）如图，在平面直角坐标系
中，椭圆
的离心率为
，
过椭圆右焦点
作两条互相垂直的弦
与
．当直线斜率为
时，
．
（Ⅰ）求椭圆的方程；
（Ⅱ）求由
、
、
、
四点构成的四边形的面积的取值范围．
(本题满分15分) 四棱锥P－ABCD中，PA⊥平面ABCD，E为AD的中点，ABCE为菱形，
∠BAD＝120°，PA＝AB，G，F分别是线段CE，PB上的动点，且满足
＝
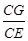＝λ∈(0，1)．
(Ⅰ) 求证：FG∥平面PDC；
(Ⅱ) 求λ的值，使得二面角F－CD－G的平面角的正切值为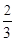
．
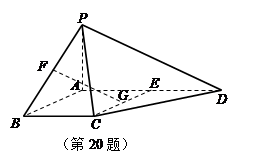
) (本题满分14分) 设等差数列{an}的首项a1为a，前n项和为Sn．
(Ⅰ) 若S1，S2，S4成等比数列，求数列{an}的通项公式；
(Ⅱ) 证明：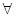
n∈N*, Sn，Sn＋1，Sn＋2不构成等比数列．
(本题满分14分) 在△ABC中，角A，B，C所对的边分别为a，b，c，已知
tan (A＋B)＝2．(Ⅰ) 求sin C的值；(Ⅱ) 当a＝1，c＝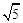
时，求b的值．
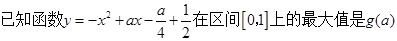
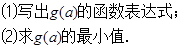
已知函数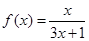
，数列
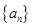满足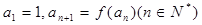
(1)证明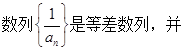
求数列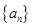的通项公式；
(2)记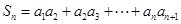
,求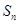
.