已知关于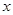
的一元二次方程
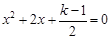有实数根，
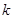为正整数．
（1）求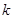的值；
（2）当此方程有两个非零的整数根时，将关于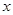的二次函数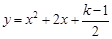
的图象向下平移9个单位，求平移后的图象的表达式；
（3）在（2）的条件下，平移后的二次函数的图象与x轴交于点A，B（点A在点B左侧），直线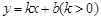
过点B，且与抛物线的另一个交点为C，直线BC上方的抛物线与线段BC组成新的图象，当此新图象的最小值大于-5时，求k的取值范围．
（共两个小题，10分）
（1）列示表示比a的3倍大4的数与比a的5倍小3的数，计算这两个数的和；
（2）已知A=2xy－2y²+8x²，B=9x²+3xy－5y²，
求 ①A－B； ②－3A+2B.
（共两个小题，每题5分，共10分）先化简，再求值：
（1）－（a²+2a）+3（a²－3a－
），其中a=－2
（2）5x²－[2xy－3（xy+2）+4x²]，其中x=－2，y=
（每小题4分，共24分）
（1）－15－（－8）+（－11）－12
（2）（－
）×（
）×
÷（－
）
（3）（－2）²+4×（－3）²－（－4）²÷（－2）
（4）－5m²n+4mn²－2mn+6m²n+3mn
（5）
ab－
+
－（－
ab）
（6）4x²－[
x－（x－3）+3x²]
如图1，在△OAB中，∠OAB=90°，∠AOB=30°，OB=8．以OB为边，在△OAB外作等边△OBC，D是OB的中点，连接AD并延长交OC于E．
（1）求证：四边形ABCE是平行四边形；
（2）如图2，将图1中的四边形ABCO折叠，使点C与点A重合，折痕为FG，求OG的长．
佳佳果品店在批发市场购买某种水果销售，第一次用1200元购进若干千克，并以每千克8元出售，很快售完．由于水果畅销，第二次购买时，每千克的进价比第一次提高了10%，用1452元所购买的数量比第一次多20千克，以每千克9元售出100千克后，因出现高温天气，水果不易保鲜，为减少损失，便降价50%售完剩余的水果．
（1）求第一次水果的进价是每千克多少元？
（2）该果品店在这两次销售中，总体上是盈利还是亏损？盈利或亏损了多少元？