如图,在直角坐标平面内,直线y=-x+5与x轴和y轴分别交于A、B两点,二次函数y=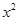 +bx+c的图象经过点A、B,且顶点为C.
+bx+c的图象经过点A、B,且顶点为C.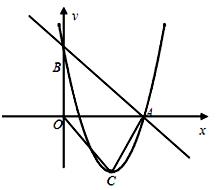
(1)求这个二次函数的解析式;
(2)求sin∠OCA的值;
(3)若P是这个二次函数图象上位于x轴下方的一点,且△ABP的面积为10,求点P的坐标.
现有5根小木棒,长度分别为:2、3、4、5、7(单位:cm),从中任意取出3根,
(1)列出所选的3根小木棒的所有可能情况;
(2)如果用这3根小木棒首尾顺次相接,求它们能搭成三角形的概率.
今年我市体育中考的现场选测项目中有一项是“排球30秒对墙垫球”,为了了解某学校九年级学生此项目平时的训练情况,随机抽取了该校部分九年级学生进行测试,根据测试结果,制作了如下尚不完整的频数分布表:
| 组别 |
垫球个数x(个) |
频数(人数) |
频率 |
| 1 |
10≤x<20 |
5 |
0.10 |
| 2 |
20≤x<30 |
a |
0.18 |
| 3 |
30≤x<40 |
20 |
b |
| 4 |
40≤x<50 |
16 |
0.32 |
| 合计 |
1 |
(1)表中a= ,b= ;
(2)这个样本数据的中位数在第 组;
(3)下表为(体育与健康)中考察“排球30秒对墙垫球”的中考评分标准,若该校九年级有500名学生,请你估计该校九年级学生在这一项目中得分在7分以上(包括7分)学生约有多少人?
排球30秒对墙垫球的中考评分标准
| 分值 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
| 排球(个) |
40 |
36 |
33 |
30 |
27 |
23 |
19 |
15 |
11 |
7 |
解不等式 x-1>2x,并把解集在数轴上表示出来
x-1>2x,并把解集在数轴上表示出来
.
化简 .
为节约用水,某市居民生活用水按阶梯式水价计量,将居民的每月生活用水水价
分为三个等级:一级20立方米及以下,二级21~30立方米(含30立方米),三级31立方
米及以上,以下是王聪家水费发票的部分信息:
| 浙江省××市自来水总公司水费专用 发票联 计费日期:2011-07-01至2011-08-01付款期限: |
||||||
| 上期抄见数 |
本期抄见数 |
加原表用水量(吨) |
本期用水量(吨) |
|||
| 889 |
924 |
35 |
||||
| 自来水费(含水资源费) |
污水处理费 |
|||||
| 用水量(吨) |
单价元(/吨) |
金额(元) |
用水量(吨) |
单价元(/吨) |
金额(元) |
|
| 阶梯一20 |
1.30 |
26.00 |
20 |
0.50 |
10.00 |
|
| 阶梯二10 |
 |
19.00 |
10 |
0.50 |
5.00 |
|
| 阶梯三5 |
 |
15.00 |
5 |
0.50 |
2.50 |
|
| 本期实付金额(大写) |
柒拾柒元伍角整77.50(元) |
|||||
(注:居民生活用水水价=居民生活自来水费+居民生活污水处理费)
(1)从以上信息可知,水费的收费标准(含污水处理费)是:每月用水20吨及以内为元
/吨,每月用水21~30吨(含30吨)为元/吨,31立方米及以上为元/吨.2.9
(2)随着气温的降低,王聪家的用水量也在逐步下降,已知2012年2月份王聪家所缴的水
费为55.20元,请你计算王聪家该月份的用水量为多少吨.
(3)2012年4月1日起,该市水价在现有的基础上上调了10%,为了节省开支,王聪家决
定把每月水费控制在家庭月收入的1.5%以内,若王聪家的月收入为5428元,则王聪家每月
的用水量最多只能用多少立方米(精确到1立方米).