如图甲,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF。解答下列问题: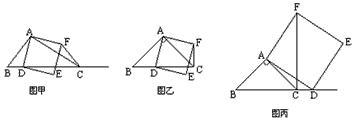
(1)如果AB=AC,∠BAC=90°。
①当点D在线段BC上时(与点B不重合),如图乙,线段CF、BD之间的位置关系为 ,数量关系为 ;
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?
(2)如果AB≠AC,∠BAC>90°,点D在线段BC上运动.试探究:请直接写出当△ABC满足一个什么条件时,CF⊥BC(点C、F重合除外),不必说明理由。
(本小题满分16分,每小题8分)
(1)解方程组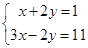
(2)解不等式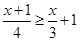
如图,已知抛物线 与直线AB相交于A(﹣3,0),B(0,3)两点.
与直线AB相交于A(﹣3,0),B(0,3)两点.
(1)求这条抛物线的解析式;
(2)设C是抛物线对称轴上的一动点,求使∠CBA=90°的点C的坐标;
(3)探究在抛物线上是否存在点P,使得△APB的面积等于3?若存在,求出点P的坐标;若不存在,请说明理由.
如图,AB是⊙O的直径,C为⊙O上一点,AC平分∠BAD,AD⊥DC,垂足为D,OE⊥AC,垂足为E.
(1)求证:DC是⊙O的切线;
(2)若OE= cm,AC=
cm,AC= cm,求DC的长(结果保留根号).
cm,求DC的长(结果保留根号).
某商场销售一批同型号的彩电,第一个月售出50台,为了减少库存,第二个月每台降价500元将这批彩电全部售出,已知第一个月的销售额与第二个月的销售额相等,这两个月销售总额超过40万元.
(1)求第一个月每台彩电销售价格;
(2)这批彩电最少有多少台?
如图,将矩形ABCD沿对角线BD对折,点C落在E处,BE与AD相交于点F.若DE=4,BD=8.
(1)求证:AF=EF;
(2)求证:BF平分∠ABD.