如图，点D，E在△ABC的边BC上，连接AD，AE．①AB=AC；②AD=AE；③BD=CE．以此三个等式中的两个作为命题的题设，另一个作为命题的结论，构成三个命题：（1）①②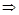
③；（2）①③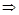②；（3）②③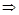①．
（1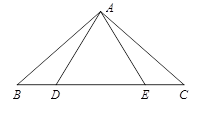）以上三个命题是真命题的为（直接写号） ；
（2）请选择一个真命题进行证明（先写出所选命题，然后证明）．
甲乙两车分别从A、B两地相向而行，甲车出发1小时后乙车出发，并以各自速度匀速行驶，两车相遇后依然按照原速度原方向各自行驶，如图所示是甲乙两车之间的距离S（千米）与甲车出发时间t（小时）之间的函数图象，其中D点表示甲车到达B地，停止行驶．
（1 ）A、B两地的距离 千米；乙车速度是 ；a表示 ．
（2）乙出发多长时间后两车相距330千米？
齐齐哈尔市教育局非常重视学生的身体健康状况，为此在体育考试中对部分学生的立定跳远成绩进行了调查（分数为整数，满分100分），根据测试成绩（最低分为53分）分别绘制了如下统计表和统计图．（如图）
| 分数 |
59.5分以下 |
59.5分以上 |
69.5分以上 |
79.5以上 |
89.5以上 |
| 人数 |
3 |
42 |
32 |
20 |
8 |
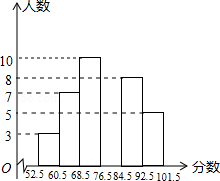
（1）被抽查的学生为 人．
（2）请补全频数分布直方图．
（3）若全市参加考试的学生大约有4500人，请估计成绩优秀的学生约有多少人？（80分及80分以上为优秀）
（4）若此次测试成绩的中位数为78分，请直接写出78.5～89.5分之间的人数最多有多少人？．
如图，已知二次函数y=ax2+bx+c的图象经过点A（﹣4，0），B（﹣1，3），C（﹣3，3）
（1）求此二次函数的解析式；
（2）设此二次函数的对称轴为直线l，该图象上的点P（m，n）在第三象限，其关于直线l的对称点为M，点M关于y轴的对称点为N，若四边形OAPN的面积为20，求m、n的值．
如图所示，在△OAB中，点B的坐标是（0，4），点A的坐标是（3，1）．
（1）画出△OAB向下平移4个单位长度、再向左平移2个单位长度后的△O1A1B1
（2）画出△OAB绕点O逆时针旋转90°后的△OA2B2，并求出点A旋转到A2所经过的路径长（结果保留π）
先化简，再求值：
，其中a、b满足式子
．