(1)引入:如图1,直线AB为⊙O的弦,OC⊥OA,交AB于点P,且PC=BC,直线BC是否与⊙O相切,为什么?
(2)引申:记(1)中⊙O的切线为直线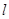 ,在(1)的条件下,如图2,将切线
,在(1)的条件下,如图2,将切线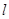 向下平移,设平移后的直线
向下平移,设平移后的直线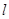 与OB的延长线相交于点
与OB的延长线相交于点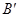 ,与AB的延长线相交于点E,与OP的延长线相交于点
,与AB的延长线相交于点E,与OP的延长线相交于点 .
.
找出图2中与 相等的线段,并说明理由;
相等的线段,并说明理由;
如果 =9cm,
=9cm,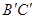 =12cm,⊙O的半径为6cm,试求线段
=12cm,⊙O的半径为6cm,试求线段 的长.
的长.
如图,抛物线 的图象经过 , , 三点.
(1)求抛物线的解析式.
(2)抛物线的顶点 与对称轴 上的点 关于 轴对称,直线 交抛物线于点 ,直线 交 于点 ,若直线 将 的面积分为 两部分,求点 的坐标.
(3) 为抛物线上的一动点, 为对称轴上动点,抛物线上是否存在一点 ,使 、 、 、 为顶点的四边形为平行四边形?若存在,求出点 的坐标;若不存在,请说明理由.

如图,在 中, , 为 边上的一点,以 为直径的 交 于点 ,交 于点 ,过点 作 交 于点 ,交 于点 ,过点 的弦 交 于点 不是直径),点 为弦 的中点,连结 , 恰好为 的切线.
(1)求证: 是 的切线.
(2)求证: .
(3)若 , ,求四边形 的面积.
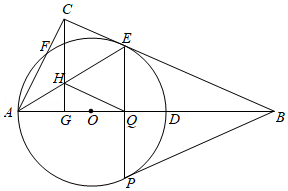
如图,在平面直角坐标系中,已知点 的坐标为 ,点 的坐标为 ,连结 ,以 为边在第一象限内作正方形 ,直线 交双曲线 于 、 两点,连结 ,交 轴于点 .
(1)求双曲线 和直线 的解析式.(2)求 的面积.
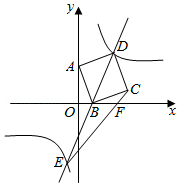
端午节是中国的传统节日.今年端午节前夕,遂宁市某食品厂抽样调查了河东某居民区市民对 、 、 、 四种不同口味粽子样品的喜爱情况,并将调查情况绘制成如图两幅不完整统计图:
(1)本次参加抽样调查的居民有 人.
(2)喜欢 种口味粽子的人数所占圆心角为 度.根据题中信息补全条形统计图.
(3)若该居民小区有6000人,请你估计爱吃 种粽子的有 人.
(4)若有外型完全相同的 、 、 、 粽子各一个,煮熟后,小李吃了两个,请用列表或画树状图的方法求他第二个吃的粽子恰好是 种粽子的概率.
阅读以下材料,并解决相应问题:
小明在课外学习时遇到这样一个问题:
定义:如果二次函数 , 、 、 是常数)与 , 、 、 是常数)满足 , , ,则这两个函数互为“旋转函数”.求函数 的旋转函数,小明是这样思考的,由函数 可知, , , ,根据 , , ,求出 , , 就能确定这个函数的旋转函数.
请思考小明的方法解决下面问题:
(1)写出函数 的旋转函数.
(2)若函数 与 互为旋转函数,求 的值.
(3)已知函数 的图象与 轴交于 、 两点,与 轴交于点 ,点 、 、 关于原点的对称点分别是 、 、 ,试求证:经过点 、 、 的二次函数与 互为“旋转函数”.