阅读以下材料,并解决相应问题:
小明在课外学习时遇到这样一个问题:
定义:如果二次函数 , 、 、 是常数)与 , 、 、 是常数)满足 , , ,则这两个函数互为“旋转函数”.求函数 的旋转函数,小明是这样思考的,由函数 可知, , , ,根据 , , ,求出 , , 就能确定这个函数的旋转函数.
请思考小明的方法解决下面问题:
(1)写出函数 的旋转函数.
(2)若函数 与 互为旋转函数,求 的值.
(3)已知函数 的图象与 轴交于 、 两点,与 轴交于点 ,点 、 、 关于原点的对称点分别是 、 、 ,试求证:经过点 、 、 的二次函数与 互为“旋转函数”.
(本题12分)阅读下列材料并解决有关问题:我们知道 ,现在我们可以用这一个结论来化简含有绝对值的代数式,如化简代数式
,现在我们可以用这一个结论来化简含有绝对值的代数式,如化简代数式 时,可令
时,可令 和
和 ,分别求得
,分别求得 (称
(称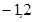 分别为
分别为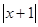 与
与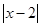 的零点值).在有理数范围内,零点值
的零点值).在有理数范围内,零点值 和
和 可将全体有理数分成不重复且不遗漏的如下3种情况:(1)当
可将全体有理数分成不重复且不遗漏的如下3种情况:(1)当 时,原式=
时,原式= ;
;
(2)当 时,原式=
时,原式= ;
;
(3)当 时,原式=
时,原式= .
.
综上讨论,原式=
通过以上阅读,请你解决以下问题:(1)求出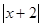 和
和 的零点值;(2)化简代数式
的零点值;(2)化简代数式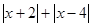
(本题10分)(1)观察一列数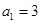 ,
,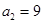 ,
, ,
,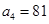 ,…,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是_______;根据此规律,如果an(n为正整数)表示这个数列的第n项,那么
,…,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是_______;根据此规律,如果an(n为正整数)表示这个数列的第n项,那么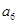 =_______,
=_______,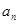 =_______;(可用幂的形式表示)
=_______;(可用幂的形式表示)
(2)如果想要求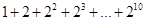 的值,可令
的值,可令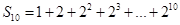 ①
①
将①式两边同乘以2,得___________②,
由②减去①式,得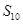 =__________________.
=__________________.
(3)若(1)中数列共有20项,设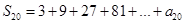 ,请利用上述规律和方法计算
,请利用上述规律和方法计算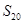 的值.(列式计算)
的值.(列式计算)
(本题8分)已知:A-2B=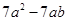 ,且B=
,且B=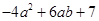 ,
,
(1)求A等于多少?
(2)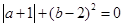 ,求A的值.
,求A的值.
(本题8分)阅读下列材料:计算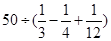 .
.
解法一:原式=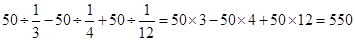 .
.
解法二:原式=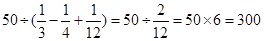 .
.
解法三:原式的倒数为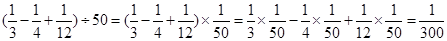 .
.
故原式=300.
上述得出的结果不同,肯定有错误的解法,你认为解法是错误的.请你选择合适的解法解答下列问题:计算: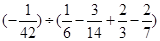
(本题10分)a、b都是正整数,设a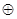 b表示从a起b个连续正整数的和,例如:2
b表示从a起b个连续正整数的和,例如:2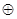 3=2+3+4,5
3=2+3+4,5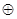 4=5+6+7+8,已知x
4=5+6+7+8,已知x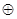 5=2005,求x的值
5=2005,求x的值