(文科)给定椭圆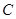 :
: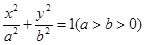 ,称圆心在原点
,称圆心在原点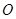 ,半径为
,半径为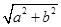 的圆是椭圆
的圆是椭圆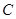 的“准圆”.若椭圆
的“准圆”.若椭圆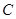 的一个焦点为
的一个焦点为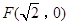 ,其短轴上的一个端点到
,其短轴上的一个端点到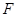 的距离为
的距离为 .
.
(Ⅰ)求椭圆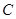 的方程和其“准圆”方程;
的方程和其“准圆”方程;
(Ⅱ)点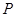 是椭圆
是椭圆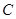 的“准圆”上的动点,过点
的“准圆”上的动点,过点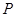 作椭圆的切线
作椭圆的切线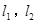 交“准圆”于点
交“准圆”于点 .
.
(ⅰ)当点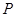 为“准圆”与
为“准圆”与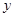 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线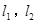 的方程并证明
的方程并证明 ;
;
(ⅱ)求证:线段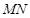 的长为定值.
的长为定值.
如图,在平面直角坐标系 中,已知椭圆
中,已知椭圆 :
: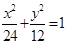 ,设
,设 是椭圆
是椭圆 上的任一点,从原点
上的任一点,从原点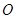 向圆
向圆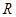 :
: 作两条切线,分别交椭圆于点
作两条切线,分别交椭圆于点 ,
,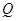 .
.
(1)若直线 ,
, 互相垂直,求圆
互相垂直,求圆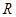 的方程;
的方程;
(2)若直线 ,
, 的斜率存在,并记为
的斜率存在,并记为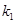 ,
,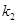 ,求证:
,求证: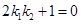 ;
;
(3)试问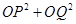 是否为定值?若是,求出该值;若不是,说明理由.
是否为定值?若是,求出该值;若不是,说明理由.
已知函数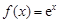 (其中
(其中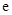 是自然对数的底数),
是自然对数的底数),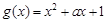 ,
,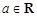 .
.
(1)记函数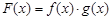 ,且
,且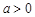 ,求
,求 的单调增区间;
的单调增区间;
(2)若对任意
 ,
, ,均有
,均有 成立,求实数
成立,求实数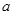 的取值范围.
的取值范围.
如图是一个半圆形湖面景点的平面示意图.已知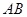 为直径,且
为直径,且 km,
km,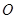 为圆心,
为圆心, 为圆周上靠近
为圆周上靠近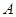 的一点,
的一点,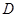 为圆周上靠近
为圆周上靠近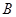 的一点,且
的一点,且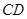 ∥
∥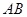 .现在准备从
.现在准备从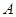 经过
经过 到
到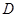 建造一条观光路线,其中
建造一条观光路线,其中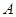 到
到 是圆弧
是圆弧 ,
, 到
到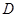 是线段
是线段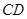 .设
.设 ,观光路线总长为
,观光路线总长为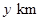 .
.
(1)求 关于
关于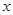 的函数解析式,并指出该函数的定义域;
的函数解析式,并指出该函数的定义域;
(2)求观光路线总长的最大值.
如图,在四棱锥 中,底面
中,底面 是菱形,且
是菱形,且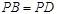 .
.
(1)求证: ;
;
(2)若平面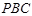 与平面
与平面 的交线为
的交线为 ,求证:
,求证: .
.
已知 的内角
的内角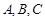 的对边分别为
的对边分别为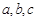 ,
,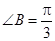 .
.
(1)若 ,
,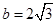 ,求
,求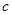 的值;
的值;
(2)若 ,求
,求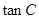 的值.
的值.