(理科)在平面直角坐标系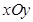 中,设点
中,设点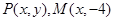 ,以线段
,以线段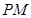 为直径的圆经过原点
为直径的圆经过原点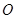 .
.
(Ⅰ)求动点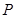 的轨迹
的轨迹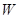 的方程;
的方程;
(Ⅱ)过点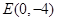 的直线
的直线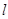 与轨迹
与轨迹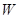 交于两点
交于两点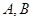 ,点
,点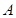 关于
关于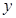 轴的对称点为
轴的对称点为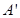 ,试判断直线
,试判断直线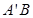 是否恒过一定点,并证明你的结论.
是否恒过一定点,并证明你的结论.
(本小题12分)
某企业为适应市场需求,准备投入资金16万元生产W和R型两种产品。经市场预测,生产W型产品所获利润 (万元)与投入资金
(万元)与投入资金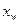 (万元)成正比例关系,且当投入资金为6万元时,可获利润1.5
(万元)成正比例关系,且当投入资金为6万元时,可获利润1.5 万元。生产R型产品所获利润
万元。生产R型产品所获利润 (万元)与投入资金
(万元)与投入资金 (
( 万元)满足关系
万元)满足关系 ,为获得最大总利润,问生产W、R型产品各应投入资金多少万元?获得的最大总利润是多少?
,为获得最大总利润,问生产W、R型产品各应投入资金多少万元?获得的最大总利润是多少?
(本小题12分)
已知奇函数 ,在
,在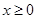 时的图象是如图所示的抛物线的一部分,
时的图象是如图所示的抛物线的一部分,
(1)请补全函数 的图象(2)求函数
的图象(2)求函数 的表达式
的表达式
(3)写出函数 的单调区间
的单调区间
(本小题12分)
已知函数 的定义域为集合A,
的定义域为集合A,
(1)求集合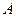 ;
;
(2)若 ,求
,求 的取值范围;
的取值范围;
(3)若全集 ,
,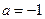 ,求
,求 及
及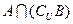
如图,在直三棱柱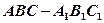 中,
中,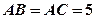 ,
,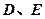 分别为
分别为 的中点,四边形
的中点,四边形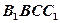 是边长为
是边长为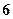 的正方形。
的正方形。
(Ⅰ)求证: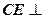 平面
平面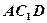 ;
;
(Ⅱ)求二面角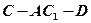 的余弦值。
的余弦值。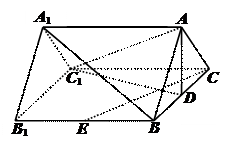
已知在四棱锥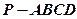 中,底面
中,底面 是矩形,且
是矩形,且 ,
,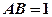 ,
, 平面
平面 ,
, 分别是线段
分别是线段 的中点。
的中点。
(Ⅰ)证明: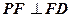 ;
;
(Ⅱ)判断并说明 上是否存在点
上是否存在点 ,使得
,使得 ∥平面
∥平面 。
。