(理科)已知椭圆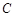 :
: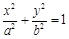 (
(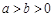 )的离心率
)的离心率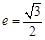 ,原点到过点
,原点到过点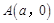 ,
,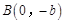 的直线的距离是
的直线的距离是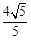 .
.
(1)求椭圆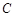 的方程;
的方程;
(2)若椭圆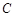 上一动点
上一动点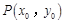 关于直线
关于直线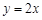 的对称点为
的对称点为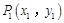 ,求
,求 的取值范围.
的取值范围.
(3)如果直线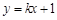 (
(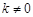 )交椭圆
)交椭圆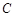 于不同的两点
于不同的两点 ,
, ,且
,且 ,
, 都在以
都在以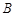 为圆心的圆上,求
为圆心的圆上,求 的值.
的值.
如图,在四边形ABCD中,
 ,,求四边形ABCD绕AD旋转一周所成几何体的表面积和体积
,,求四边形ABCD绕AD旋转一周所成几何体的表面积和体积
某租赁公司拥有汽车100辆,当每辆车每月租金为3000元时,可全部租出,当每辆车的月租金增加50元时,未租出的车将增一辆. 租出的车每辆每月需维护费150元,未租出的车的每辆每月需保管费50元,问
(1)当每辆车的月租金定为3600元时,能租出去多少辆车?
(2)每辆车的月租金为多少元时,租赁公司的月收益最大,最大是多少?
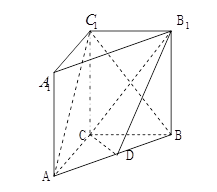
如图, 在三棱柱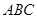 -
- 中,侧棱
中,侧棱 垂直于底面
垂直于底面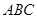 ,
,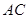 =3,
=3, =4,
=4,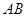 =5,
=5,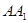 =4
=4 点D是
点D是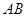 的中点,
的中点,
(1)求证: 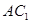 //平面
//平面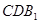 ;
;
(2)求证: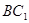 ⊥平面
⊥平面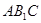 。
。
已知圆 和
和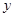 轴相切,圆心在直线
轴相切,圆心在直线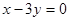 上,且被直线
上,且被直线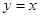 截得的弦长为
截得的弦长为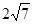
 ,求圆
,求圆 的方程
的方程
已知函数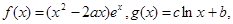
 是函数
是函数 的极值点,其中
的极值点,其中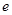 是自然对数的底数。
是自然对数的底数。
(I)求实数a的值;
(II)直线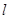 同时满足:
同时满足:
① 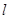 是函数
是函数 的图象在点
的图象在点 处的切线 ,
处的切线 ,
② 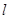 与函数
与函数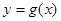 的图象
的图象 相切于点
相切于点
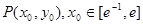 ,求实数b的取值范围
,求实数b的取值范围