(本小题满分12分)已知圆 :
: ,直线
,直线 过定点
过定点 .
.
(Ⅰ)若 与圆
与圆 相切,求
相切,求 的方程;
的方程;
(Ⅱ)若 与圆
与圆 相交于
相交于 、
、 两点,求
两点,求 的面积的最大值,并求此时直线
的面积的最大值,并求此时直线 的方程.
的方程.
(1)已知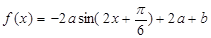 ,
,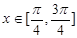 ,是否存在常数
,是否存在常数 时,使得
时,使得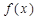 的值域为[
的值域为[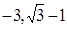 ]?若存在,求出
]?若存在,求出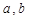 的值,若不存在,说明理由。
的值,若不存在,说明理由。
(2)若关于 的方程
的方程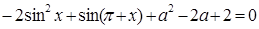 在
在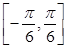 内有实数根,求实数
内有实数根,求实数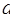 的范围。
的范围。
圆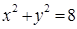 内有一点
内有一点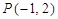 ,
,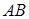 为过点
为过点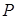 且倾斜角为
且倾斜角为 的弦,
的弦,
(1)当 =1350时,求
=1350时,求 ;
;
(2)当弦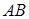 被点
被点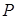 平分时,求出直线
平分时,求出直线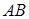 的方程;
的方程;
(3)设过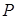 点的弦的中点为
点的弦的中点为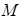 ,求点
,求点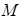 的轨迹方程.
的轨迹方程. 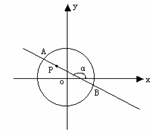
如图,在平面直角坐标系中,锐角 和钝角
和钝角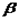 的终边分别与单位圆交于
的终边分别与单位圆交于 ,
,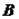 两点.
两点.
(1)如果 、
、 两点的纵坐标分别为
两点的纵坐标分别为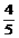 、
、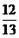 ,求
,求 和
和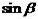 ;
;
(2)在(1)的条件下,求 的值;
的值;
(3)已知点
 ,求函数f(
,求函数f( )=
)= 的值域.
的值域.
在△ABC中,角A、B、C所对的边分别为a,b,c,且满足csinA=acosC.
(1)求角C的大小;
(2)求sinA+cosA的最大值,并求取得最大值时角A,B的大小.
如图:在三棱锥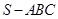 中,已知点
中,已知点 、
、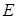 、
、 分别为棱
分别为棱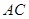 、
、 、
、 的中点.
的中点.
(1)求证: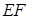 ∥平面
∥平面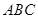 ;
;
(2)若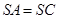 ,
,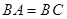 ,求证:平面
,求证:平面 ⊥平面
⊥平面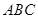 .
.