已知公比不为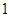 的等比数列
的等比数列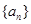 的首项
的首项 ,前
,前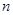 项和为
项和为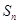 ,且
,且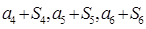 成等差数列.
成等差数列.
(1)求等比数列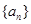 的通项公式;
的通项公式;
(2)对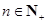 ,在
,在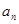 与
与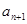 之间插入
之间插入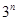 个数,使这
个数,使这 个数成等差数列,记插入的这
个数成等差数列,记插入的这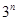 个数的和为
个数的和为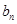 ,求数列
,求数列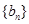 的前
的前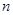 项和
项和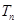 .
.
证明: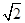 ,
,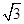 ,
,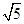 不能为同一等差数列中的三项.
不能为同一等差数列中的三项.
设a、b、c均为大于1的正数,且ab=10,求证:logac+logbc≥4lgc.
数列{an}的前n项和记为Sn,已知a1=1,an+1=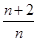 Sn(n=1,2,3,…),证明:
Sn(n=1,2,3,…),证明:
(1)数列 是等比数列;
是等比数列;
(2)Sn+1=4an.
设数列 满足a1=0且
满足a1=0且 -
-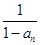 = 1.
= 1.
(1) 求 的通项公式;
的通项公式;
(2) 设bn= ,记Sn=
,记Sn= ,证明:Sn<1.
,证明:Sn<1.
设同时满足条件:① ≤bn+1(n∈N*);②bn≤M(n∈N*,M是与n无关的常数)的无穷数列{bn}叫“特界” 数列.
≤bn+1(n∈N*);②bn≤M(n∈N*,M是与n无关的常数)的无穷数列{bn}叫“特界” 数列.
(1) 若数列{an}为等差数列,Sn是其前n项和,a3=4,S3=18,求Sn;
(2) 判断(1)中的数列{Sn}是否为“特界” 数列,并说明理由.