(本小题满分14分)已知函数 .
.
(Ⅰ)求证:曲线 在点
在点 处的切线在
处的切线在 轴上的截距为定值;
轴上的截距为定值;
(Ⅱ)若 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分8分)
已知函数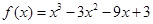 ,若函数
,若函数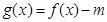 在
在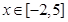 上有3个零点,求实数
上有3个零点,求实数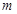 的取值范围.
的取值范围.
(本小题满分8分)
m取何值时,复数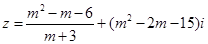
(1)是实数;(2)是纯虚数.
(12分) 22.已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,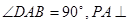
底面ABCD,PA=AD=DC=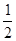 AB=1,M是PB的中点
AB=1,M是PB的中点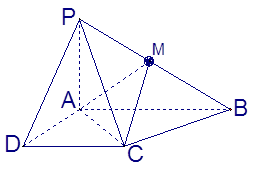
(Ⅰ)证明:面PAD⊥面PCD;
(Ⅱ)求异面直线CM与AD所成角的正切值;
(Ⅲ)求面MAC与面BAC所成二面角的正切值
.已知圆C: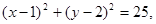
直线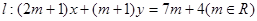
(1)证明:不论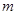 取何实数,直线
取何实数,直线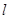 与圆C恒相交;
与圆C恒相交;
(2)求直线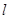 被圆C所截得的弦长最小时直线
被圆C所截得的弦长最小时直线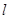 的方程;
的方程;
已知数列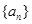 满足:
满足: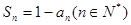 ,其中
,其中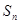 为
为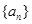 的前n项和.
的前n项和.
(1)求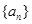 的通项公式;
的通项公式;
(2)若数列 满足
满足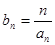 ,求
,求 的前n项和Tn.
的前n项和Tn.