(本小题满分12分)已知向量 ,
,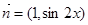 ,函数
,函数 .
.
(Ⅰ)求函数f (x)的最小正周期和单调递减区间;
(Ⅱ)在 中,
中,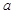 ,
, ,
, 分别是角
分别是角 ,
, ,
,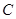 的对边,且
的对边,且 ,
, ,
, 的面积为
的面积为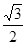 ,且a > b,求
,且a > b,求 的值.
的值.
设y=f(x)是二次函数,方程f(x)=0有两个相等的实根,且f′(x)=2x+2.
(1)求y=f(x)的表达式;
(2)求y=f(x)的图象与两坐标轴所围成图形的面积.
如图1-7-9所示,从地面垂直发射质量为m的物体,计算物体从A点飞到B点的过程中,地球引力所做的功.若要物体飞离地球引力的范围,物体的初速度v0应为多少?
图1-7-9
设一物体从初速度为1时开始做直线运动,已知在任意时刻t时的加速度为 s+1,将位移表示为时间t的函数式.
s+1,将位移表示为时间t的函数式.
在底面积为S的圆柱形容器中盛有一定量的气体,在等温条件下,由于气体的膨胀,把容器中的一个活塞(面积为S)从点a处推到b处.计算在移动过程中,气体压力所做的功.
直线y=kx将抛物线y=x-x2与x轴所围的图形分为面积相等的两部分,求k的值及直线方程.