(本小题满分12分)某校为进行爱国主义教育,在全校组织了一次有关钓鱼岛历史知识的竞赛.现有甲、乙两队参加钓鱼岛知识竞赛,每队3人,规定每人回答一个问题,答对为本队赢得1分,答错得0分.假设甲队中每人答对的概率均为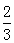 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为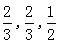 ,且各人回答正确与否相互之间没有影响,用ξ表示甲队的总得分.
,且各人回答正确与否相互之间没有影响,用ξ表示甲队的总得分.
(Ⅰ)求随机变量ξ的分布列和数学期望;
(Ⅱ)用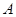 表示“甲、乙两个队总得分之和等于3”这一事件,用
表示“甲、乙两个队总得分之和等于3”这一事件,用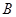 表示“甲队总得分大于乙队总得分” 这一事件,求
表示“甲队总得分大于乙队总得分” 这一事件,求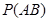 .
.
(本小题满分12分)
某污水处理厂预计2010年底投入200万元,购入一套污水处理设备,该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加1万元。
(1)求该污水处理厂使用该设备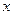 年的年平均费用
年的年平均费用 (万元);
(万元);
(2)为使该污水处理厂的年平均费用最低,该污水处理厂几年后需要重新更换新的污水处理设备?
(本小题满分12分)
一袋中装有分别标记着1,2,3,4,5数字的5个球,
(1)从袋中一次取出2个球,试求2个球中最大数字为4的概率;
(2)从袋中每次取出一个球,取出后放回,连续取2次,试求取出的2个球中最大数字为5的概率。
(本小题满分12分)
用循环语句For语句写出 的算法,并画出它的算法框图。
的算法,并画出它的算法框图。
(本小题满分12分)
已知点 、
、 、
、 的坐标分别为
的坐标分别为
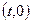 ,
, ,
, (
( ),其中
),其中 ,
,
(1)若 ,
, 的值;
的值;
(2)记 ,若
,若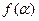 的最大值为
的最大值为 ,求实数
,求实数 的值.
的值.
(本小题满分12分)
甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 7978 95 88 93 84
乙 92 95 80 75 83 80 90 85
(1)用茎叶图表示这两组数据;若将频率视为概率,对甲学生在培训后参加的一次数学竞赛成绩进行预测,求甲的成绩高于80分的概率;
(2)现要从中选派一人参加数学竞赛,从统计学的角度(在平均数、方差或标准差中选两个)考虑,你认为选派哪位学生参加合适?请说明理由.
标准差公式: .
.