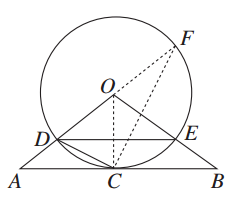
如图，AB为圆O的切线，A为切点，C为线段AB的中点，过C作圆O的割线CED（E在C，D之间），求证：∠CBE=∠BDE．
已知x，y为正实数，满足1≤lg(xy)≤2,3≤lg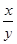
≤4，求lg(x4y2)的取值范围．
已知关于x的不等式(ax－5)(x2－a)<0的解集为M.
(1)当a＝4时，求集合M；
(2)当3∈M，且5∉M时，求实数a的取值范围．
已知a>b>0，比较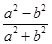
与
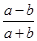的大小．
如图，圆O的直径AB＝8，圆周上过点C的切线与BA的延长线交于点E，过点B作AC的平行线交EC的延长线于点P．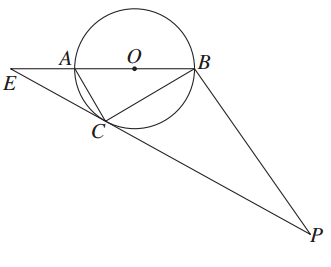
(1)求证：BC2＝AC·BP；
(2)若EC＝2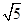
，求PB的长．
如图，△ABO三边上的点C、D、E都在⊙O上，已知AB∥DE，AC＝CB．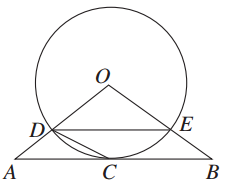
(1)求证：直线AB是⊙O的切线；
(2)若AD＝2，且tan∠ACD＝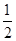
，求⊙O的半径r的长．