(本小题满分12分)已知函数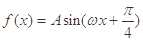 (其中
(其中 ,
, ,
, )的最大值为2,最小正周期为
)的最大值为2,最小正周期为 .
.
(Ⅰ)求函数 的解析式及函数的增区间;
的解析式及函数的增区间;
(Ⅱ)若函数 图象上的两点
图象上的两点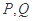 的横坐标依次为
的横坐标依次为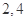 ,
,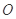 为坐标原点,求△
为坐标原点,求△ 的面积.
的面积.
(本小题满分12分)
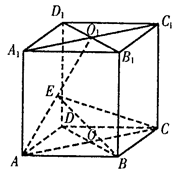
如图,直平行六面体ABCD-A1B1C1D1的高为3,
底面是边长为4, 且∠BAD=60°的菱形,AC∩
BD=O,A1C1∩B1D1=O1,E是线段AO1上一点.
(Ⅰ)求点A到平面O1BC的距离;
(Ⅱ)当AE为何值时,二面角E-BC-D的大小为 .
.
(本小题满分10分)
如图,设A是单位圆和x轴正半轴的交点,P,Q是单
位圆上的两点,D是坐标原点,∠AOP=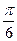 .∠AOQ=α,α∈[0,π).(Ⅰ)若Q(
.∠AOQ=α,α∈[0,π).(Ⅰ)若Q(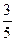 ,
,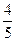 ),求cos(α-
),求cos(α-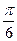 )的值; (Ⅱ)设函数f(α)=
)的值; (Ⅱ)设函数f(α)=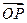 ·
·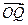 ,求f(α)的值域.
,求f(α)的值域.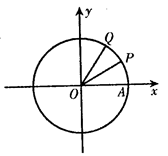
(本小题满分12分)
对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点。如果函数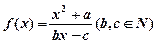 有且只有两个不动点0,2,且
有且只有两个不动点0,2,且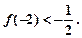
(1)求函数f(x)的解析式;
(2)已知各项不为零的数列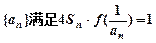 (
(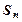 为
为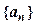 数列前n项和),求数列通项
数列前n项和),求数列通项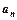 ;
;
(3)如果数列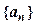 满足
满足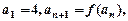 ,求证:当
,求证:当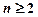 时,恒有
时,恒有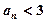 成立.
成立.
已知椭圆
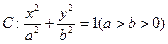 过点
过点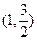 ,且离心率
,且离心率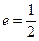 ,
,
(Ⅰ)求椭圆方程;
(Ⅱ)若直线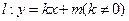 与椭圆交于不同的两点
与椭圆交于不同的两点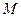 .
.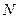 ,且线段
,且线段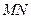 的垂直平分线过定点
的垂直平分线过定点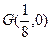 ,求
,求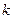 的取值范围。
的取值范围。
数列{an}满足a1=1,a2=2,an+2=(1+cos2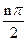 )an+sin
)an+sin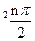 ,n=1.2.3…
,n=1.2.3…
(1)求a3.a4并求数列{an}的通项公式
(2)设bn=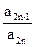 ,令 Sn=
,令 Sn=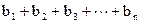 ,求 Sn
,求 Sn