(本小题满分10分)选修4—1:几何证明选讲
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.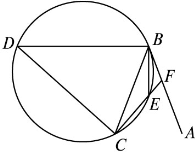
(1)证明:DB=DC;
(2)设圆的半径为1,BC=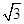 ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.
(理科)设椭圆E: 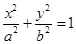 (a,b>0)过M(2,
(a,b>0)过M(2, ),N(
),N( ,1)两点,O为坐标原点,
,1)两点,O为坐标原点,
(Ⅰ)求椭圆E的方程;
(Ⅱ)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且 ?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理由。
?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理由。
(文科)已知椭圆的一个顶点为(﹣2,0),焦点在x轴上,且离心率为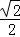 .
.
(1)求椭圆的标准方程.
(2)斜率为1的直线l与椭圆交于A、B两点,O为原点,当△AOB的面积最大时,求直线l的方程.
(理科)椭圆 的离心率为
的离心率为 ,
, 轴被曲线
轴被曲线 截得的线段长等于
截得的线段长等于 的长半轴长。
的长半轴长。
(Ⅰ)求 ,
, 的方程;
的方程;
(Ⅱ)设 与
与 轴的交点为M,过坐标原点O的直线
轴的交点为M,过坐标原点O的直线 与
与 相交于点A,B,直线MA,MB分别与
相交于点A,B,直线MA,MB分别与 相交与D,E.
相交与D,E.
(ⅰ)证明: ;
;
(ⅱ)记△MAB,△MDE的面积分别是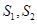 .问:是否存在直线
.问:是否存在直线 ,使得
,使得 =
=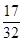 ?
?
(文科)已知椭圆的中心在坐标原点,两个顶点在直线x+2y﹣4=0上,F1是椭圆的左焦点.
(1)求椭圆的标准方程;
(2)设点P是椭圆上的一个动点,求线段PF1的中点M的轨迹方程;
(3)若直线l:y=x+m与椭圆交于点A,B两点,求△ABO面积S的最大值及此时直线l的方程.
(理科)在平面直角坐标系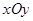 中,已知点
中,已知点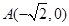 ,
, ,
, 为动点,且直线
为动点,且直线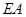 与直线
与直线 的斜率之积为
的斜率之积为 .
.
(Ⅰ)求动点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)设过点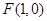 的直线
的直线 与曲线
与曲线 相交于不同的两点
相交于不同的两点 ,
, .若点
.若点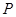 在
在 轴上,且
轴上,且 ,求点
,求点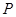 的纵坐标的取值范围.
的纵坐标的取值范围.