26．甲乙两人在相同条件下各射靶10次，甲10次射靶的成绩的情况如图所示，乙10次射靶的成绩依次是：3环、4环、5环、8环、7环、7环、8环、9环、9环、10环．
（1）请在图中画出乙的射靶成绩的折线图．
（2）请将下表填完整：
| |
平均数 |
方差 |
中位数 |
命中9环及以上次数 |
| 甲 |
7 |
1.2 |
|
|
| 乙 |
|
4.8 |
|
3 |
（3）请从下列三个不同角度对这次测试结果进行分析．
①从平均数和方差相结合看（分析谁的成绩稳定些）；
②从平均数和中位数相结合看（分析谁的成绩好些）．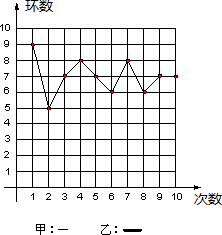
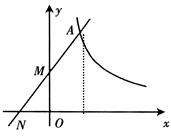
直线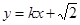
与反比例函数
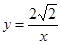(x>0)的图像交于点A，与坐标轴分别交于M、N两点，当AM=MN时,求k的值.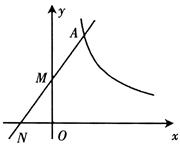
正方形ABCD的边长为3，E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°，得到△DCM.
（1）求证：EF="FM"
（2）当AE=1时，求EF的长．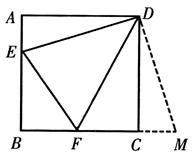
在⊙O中，直径AB⊥CD于点E，连接CO并延长交AD于点F,且CF⊥AD.
求∠D的度数.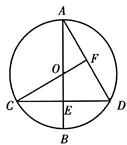
商场对每个营业员在当月某种商品销售件数统计如下：
解答下列问题
（1）设营业员的月销售件数为x(单位:件),商场规定:当x＜15时为不称职；当15≤x＜20时为基本称职；当20≤x＜25为称职；当x≥25时为优秀.试求出优秀营业员人数所占百分比；
（2）根据（1）中规定，计算所有优秀和称职的营业员中月销售件数的中位数和众数；
（3）为了调动营业员的工作积极性，商场决定制定月销售件数奖励标准，凡达到或超过这个标准的营业员将受到奖励。如果要使得所有优秀和称职的营业员中至少有一半能获奖，你认为这个奖励标准应定为多少件合适？并简述其理由.
某商场为了吸引顾客，设计了一种促销活动，在一个不透明的箱子里放有4个相同的小球，在球上分别标有“0元”、“10元”、“20元”、“30元”的字样，规定：顾客在本商场同一天内，每消费满200元，就可以在箱子里先后摸出两个球（第一次摸出后不放回）.商场根据两小球所标金额的和，返还相应价格的购物券，可以重新在本商场消费.某顾客刚好消费200元.
（1）该顾客至少可得到元购物券，至多可得到元购物券；
（2）请你用画树状图或列表的方法，求出该顾客所获得购物券的金额不低于30元的概率