已知⊙O过点D(4,3),点H与点D关于x轴对称,过H作⊙O的切线交x轴于点A.
(1)求sin∠HAO的值;
(2)如图,设⊙O与x轴正半轴交点为P,点E、F是线段OP上的动点(与点P不重合),连接并延长DE、DF交⊙O于点B、C,直线BC交x轴于点G,若△DEF是以EF为底的等腰三角形,试探索sin∠CGO的大小怎样变化,请说明理由.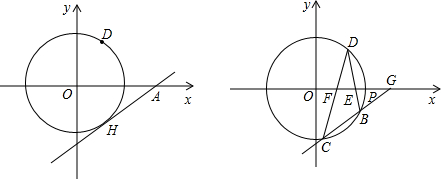
如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形 ABE.点F是对角线BD上一动点(点F不与点B重合),将线段AF绕点A顺时针方向旋转60°得到线段AM,连接FM.
(1)求AO的长;
(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AC= AM;
AM;
(3)连接EM,若△AEM的面积为40,请直接写出△AFM的周长.
如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).
已知直线y=﹣3x与双曲线y= 交于点P (﹣1,n).
交于点P (﹣1,n).
(1)求m的值;
(2)若点A ( ,
, ),B(
),B( ,
, )在双曲线y=
)在双曲线y= 上,且
上,且 <
< <0,试比较
<0,试比较 ,
, 的大小.
的大小.
某中学为了预测本校应届毕业女生“一分钟跳绳”项目考试情况,从九年级随机抽取部分女生进行该项目测试,并以测试数据为样本,绘制出如图10所示的部分频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值)和扇形统计图.根据统计图提供的信息解答下列问题: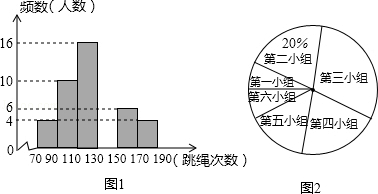
(1)补全频数分布直方图,并指出这个样本数据的中位数落在第 小组;
(2)若测试九年级女生“一分钟跳绳”次数不低于130次的成绩为优秀,本校九年级女生共有260人,请估计该校九年级女生“一分钟跳绳”成绩为优秀的人数;
(3)如测试九年级女生“一分钟跳绳”次数不低于170次的成绩为满分,在这个样本中,从成绩为优秀的女生中任选一人,她的成绩为满分的概率是多少?
如图,AB,AC分别是半⊙O的直径和弦,OD⊥AC于点D,过点A作半⊙O的切线AP,AP与OD的延长线交于点P.连接PC并延长与AB的延长线交于点F.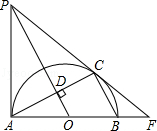
(1)求证:PC是半⊙O的切线;
(2)若∠CAB=30°,AB=10,求线段BF的长.