（本小题满分10分）为了研究某种细菌在特定环境下，随时间变化繁殖情况，得如下实验数据：
| 天数t（天） |
3 |
4 |
5 |
6 |
7 |
| 繁殖个数y（千个） |
2．5 |
3 |
4 |
4．5 |
6 |
（Ⅰ）求y关于t的线性回归方程；
（Ⅱ）利用（Ⅰ）中的回归方程，预测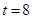
时，细菌繁殖个数．
附：回归直线的斜率和截距的最小二乘法估计公式分别为：
，
．
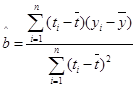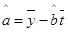如图，三棱柱
中，
平面
，
，
, 点
在线段
上，且
，
．
（Ⅰ）求证：直线
与平面不平行；
（Ⅱ）设平面
与平面所成的锐二面角为
，若
，求
的长；
（Ⅲ）在（Ⅱ）的条件下，设平面
平面
，求直线
与所成的角的余弦值．
已知数列
的前
项和为
，且
．
（1）求的通项公式；
（2）设
，若
恒成立，求实数
的取值范围；
（3）设
,
是数列
的前项和，证明
．
设函数
，
（Ⅰ）求
的最大值，并写出使取最大值时x的集合；
（Ⅱ）已知
中，角A、B、C的对边分别为a、b、c，若
，
，求的面积的最大值．
已知函数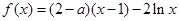
，
，（
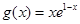为自然对数的底数）.
（1）若不等式
对于一切
恒成立，求a的最小值；
（2）若对任意的
，在
上总存在两个不同的
，使
成立，求a的取值范围.
已知函数
的导数
，曲线
在点
处的切线方程为
.
（1）求b，c的值；
（2）求函数的单调区间；
（3）设函数
，且
在区间
内存在单调递减区间，求实数a的取值范围.