（本小题满分10分）某校数学课外兴趣小组为研究数学成绩是否与性别有关，先统计本校高三年级每个学生一学期数学成绩平均分（采用百分制），剔除平均分在30分以下的学生后，共有男生300名，女生200名．现采用分层抽样的方法，从中抽取了100名学生，按性别分为两组，并将两组学生成绩分为6组，得到如下所示频数分布表．
| 分数段 |
[40，50） |
[50，60） |
[60，70） |
[70，80） |
[80，90） |
[90，100] |
| 男 |
3 |
9 |
18 |
15 |
6 |
9 |
| 女 |
6 |
4 |
5 |
10 |
13 |
2 |
估计男、女生各自的成绩平均分（同一组数据用该组区间中点值作代表），从计算结果看，判断数学成绩与性别是否有关；
| |
优分 |
非优分 |
合计 |
| 男生 |
|
|
|
| 女生 |
|
|
|
| 合计 |
|
|
100 |
（2）规定80分以上为优分（含80分），请你根据已知条件作出
列联表，并判断是否有
以上的把握认为“数学成绩与性别有关”．
附表及公式
 |
0．100 |
0．050 |
0．010 |
0．001 |
 |
2．706 |
3．841 |
6．635 |
10．828 |
．
已知椭圆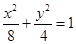
，过点
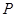
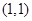作直线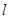
与椭圆交于
、
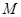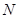两点.
（1）若点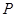平分线段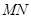
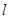，试求直线的方程；
设与满足（1）中条件的直线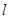平行的直线与椭圆交于
、
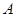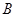两点，
与椭圆交于点
，
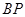与椭圆交于点
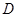，求证：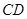
//
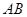
如图，在底面是正方形的四棱锥P－ABCD中，PA⊥面ABCD，BD交AC于点E，F是PC中点，G为AC上一点．
(1)求证：BD⊥FG；
(2)确定点G在线段AC上的位置，使FG∥平面PBD，并说明理由；
(3)当二面角B－PC－D的大小为
时，求PC与底面ABCD所成角的正切值
某工厂对200个电子元件的使用寿命进行检查，按照使用寿命(单位：h)，
可以把这批电子元件分成第一组[100,200]，第二组(200,300]，第三组(300,400]，第四组(400,500]，第五组(500,600]，第六组(600,700]．由于工作中不慎将部分数据丢失，现有以下部分图表：
| 分组 |
[100,200] |
(200,300] |
(300,400] |
(400,500] |
(500,600] |
(600,700] |
| 频数 |
B |
30 |
E |
F |
20 |
H |
| 频率 |
C |
D |
0.2 |
0.4 |
G |
I |
(1)求图2中的A及表格中的B，C，D，E，F，G，H，I的值；
(2)求图2中阴影部分的面积；
(3)若电子元件的使用时间超过300h为合格产品，求这批电子元件合格的概率
已知椭圆
，
分别为左顶点和上顶点，F为右焦点，过F作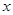
轴的垂线交椭圆于点C，且直线
与直线OC平行.
（1）求椭圆的离心率；
（2）已知定点M（
），
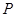为椭圆上的动点，若
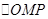的重心轨迹经过点
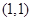，求椭圆的方程.
甲打靶射击，有4发子弹，其中有一发是空弹（“空弹”即只有弹体没有弹头的子弹）.
（1）如果甲只射击
次，求在这一枪出现空弹的概率；
（2）如果甲共射击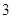
次，求在这三枪中出现空弹的概率；
（3）如果在靶上画一个边长为
的等边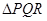
，甲射手用实弹瞄准了三角形
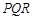区域随机射击，且弹孔都落在三角形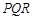内。求弹孔与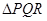三个顶点的距离都大于1的概率（忽略弹孔大小）.