【原创】(本小题满分12分)将函数 (x∈R)的图像向左平移
(x∈R)的图像向左平移 个单位长度后,所得到的图像关于y轴对称,
个单位长度后,所得到的图像关于y轴对称,
(1)求 的最小值;(2)在(1)的条件下,求函数
的最小值;(2)在(1)的条件下,求函数 的单调减区间。
的单调减区间。
(选修4—5不等式证明选讲)
对于任意实数
 和
和 ,不等式
,不等式 恒成立,试求实数
恒成立,试求实数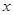 的取值范围.
的取值范围.
(选修4—4 参数方程与极坐标)
在极坐标系下,已知圆O: 和直线
和直线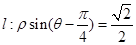 ,
,
(Ⅰ)求圆O和直线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)当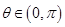 时,求直线
时,求直线 与圆O公共点的一个极坐标.
与圆O公共点的一个极坐标.
(选修4—2矩阵与变换)
变换 是将平面上每个点
是将平面上每个点 的横坐标乘2,纵坐标乘4,变到点
的横坐标乘2,纵坐标乘4,变到点 。
。
(Ⅰ)求变换 的矩阵;
的矩阵;
(Ⅱ)圆 在变换
在变换 的作用下变成了什么图形?
的作用下变成了什么图形?
(本小题满分14分)已知函数 同时满足如下三个条件:①定义域为
同时满足如下三个条件:①定义域为 ;②
;② 是偶函数;③
是偶函数;③ 时,
时,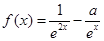 ,其中
,其中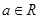 .
.
(Ⅰ)求 在
在 上的解析式,并求出函数
上的解析式,并求出函数 的最大值;
的最大值;
(Ⅱ)当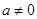 ,
,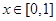 时,函数
时,函数 ,若
,若 的图象恒在直线
的图象恒在直线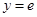 上方,求实数
上方,求实数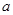 的取值范围(其中
的取值范围(其中 为自然对数的底数,
为自然对数的底数,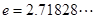 ).
).
(本小题满分13分)已知两点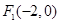 ,
, ,曲线
,曲线 上的动点
上的动点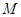 满足
满足 ,直线
,直线 与曲线
与曲线 交于另一点
交于另一点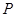 .
.
(Ⅰ)求曲线 的方程;
的方程;
(Ⅱ)设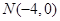 ,若
,若
 ,求直线
,求直线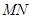 的方程.
的方程.