（本小题满分16分）某仓库为了保持库内温度，四周墙上装有如图所示的通风设施，该设施的下部是等边三角形ABC，其中AB=2米，上部是半圆，点E为AB的中点．△EMN是通风窗，（其余部分不通风）MN是可以沿设施的边框上下滑动且保持与AB平行的伸缩杆（MN和AB不重合）．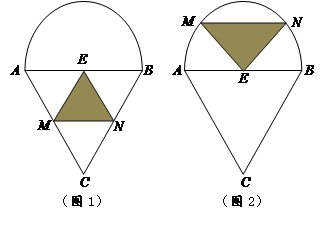
（1）设MN与C之间的距离为x米，试将△EMN的面积S表示成
的函数
；
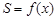（2）当MN与C之间的距离为多少时，△EMN面积最大？并求出最大值．
（本小题满分14分）若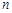
为正整数，试比较
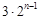与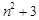
的大小，分别取
加以试验，根据试验结果猜测一个一般性结论，并用数学归纳法证明．
（本小题满分14分）如图，已知四棱锥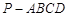
中，底面
为矩形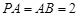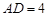，侧棱
， 
，
，
为侧棱
的中点．
（1）求异面直线
与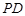
所成角的余弦值；
（2）求二面角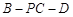
的余弦值．
（本小题满分14分）如图，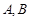
两点之间有5条网线并联，它们能通过的信息量分别为2、3、3、4、4．现从中随机任取2条网线．
（1）设选取的2条网线由
到
通过的信息总量为
，当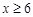
时，则保证信息畅通．求线路信息畅通的概率；
（2）求选取的2条网线可通过信息总量的数学期望．
已知函数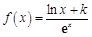
（其中
是自然对数的底数），
为
导函数．
（1）当
时，求曲线
在点
处的切线方程；
（2）若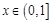
时，方程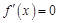
有解，求实数
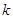的取值范围；
（3）若
，试证明：对任意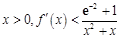
恒成立．
内有两个不同根
，求
的值及k的取值范围．