(本小题满分12分)如图,在平面直角坐标系xoy中,角α的始边与x轴的非负半轴重合且与单位圆相交于A点,它的终边与单位圆相交于x轴上方一点B,始边不动,终边在运动.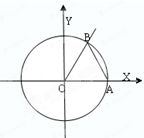
(1)若点B的横坐标为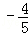 ,求tanα的值;
,求tanα的值;
(2)若△AOB为等边三角形,写出与角α终边相同的角β的集合;
(3)若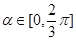 ,请写出弓形AB的面积S与α的函数关系式.
,请写出弓形AB的面积S与α的函数关系式.
已知定义在区间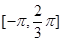 上的函数
上的函数 的图像关于直线
的图像关于直线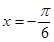 对称,当
对称,当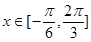 时,函数
时,函数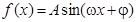
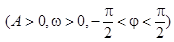 的图像如下图所示。
的图像如下图所示。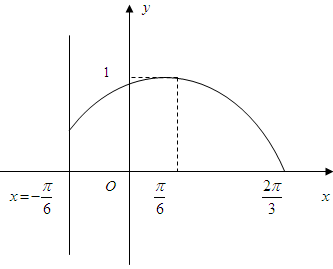
(Ⅰ) 求函数 在
在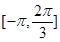 上的解析式;
上的解析式;
|
(Ⅱ) 求方程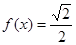 的解.
的解.
在△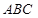 中,
中,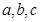 分别为三个内角
分别为三个内角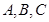 的对边,
的对边,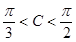 ,且
,且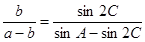 .
.
(Ⅰ) 判断△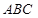 的形状;
的形状;
(Ⅱ) 若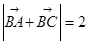 ,求
,求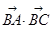 的取值范围.
的取值范围.
某市电视台为了宣传举办问答活动,随机对该市15~65岁的人群抽样了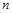 人,回答问题统计结果如图表所示.
人,回答问题统计结果如图表所示.
| 组号 |
分组 |
回答正确 的人数 |
回答正确的人数 占本组的概率 |
| 第1组 |
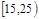 |
5 |
0.5 |
| 第2组 |
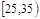 |
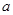 |
0.9 |
| 第3组 |
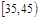 |
27 |
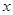 |
| 第4组 |
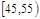 |
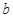 |
0.36 |
| 第5组 |
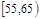 |
3 |
 |
(Ⅰ) 分别求出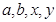 的值;
的值;
(Ⅱ) 从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组应各抽取多少人?
(Ⅲ) 在(Ⅱ)的前提下,电视台决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.
已知向量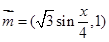 ,
,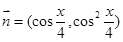 ,
,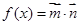
(Ⅰ)若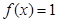 ,求
,求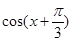 的值;
的值;
(Ⅱ)在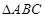 中,角
中,角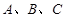 的对边分别是
的对边分别是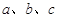 ,且满足
,且满足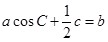 ,求函数
,求函数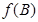 的取值范围.
的取值范围.
从某批产品中,有放回地抽取产品二次,每次随机抽取1件,假设事件 :“取出的2件产品中至多有1件是二等品”的概率
:“取出的2件产品中至多有1件是二等品”的概率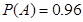 .
.
(Ⅰ) 求从该批产品中任取1件是二等品的概率 ;
;
(Ⅱ) 若该批产品共100件,从中依次抽取2件,求事件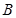 :“取出的2件产品中至少有一件二等品”的概率
:“取出的2件产品中至少有一件二等品”的概率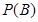 .
.