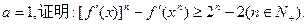已知函数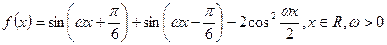
(1)求函数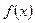 的值域
的值域
(2)若函数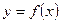 的图像与直线
的图像与直线 的两个相邻交点间的距离为
的两个相邻交点间的距离为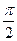 ,求函数
,求函数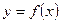 的单调增区间。
的单调增区间。
(本小题满分10分)
已知p:  是
是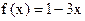 的反函数, 且
的反函数, 且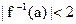 ;q : 集合
;q : 集合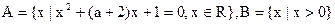 且
且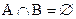 .求实数
.求实数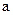 的取值范围, 使p, q中有且只有一个真命题.
的取值范围, 使p, q中有且只有一个真命题.
(本小题满分12分)
设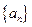 为等比数列,且其满足:
为等比数列,且其满足: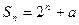 .
.
(1)求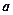 的值及数列
的值及数列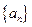 的通项公式;
的通项公式;
(2)已知数列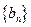 满足
满足 ,求数列
,求数列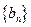 的前n项和
的前n项和 .
.
(本小题满分12分)
已知数列 ,且
,且 是函数
是函数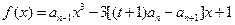 ,(
,( )的一个极值点.数列
)的一个极值点.数列 中
中 (
(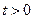 且
且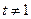 ).
).
(1)求数列 的通项公式;
的通项公式;
(2)记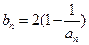 ,当
,当 时,数列
时,数列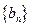 的前
的前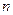 项
项 和为
和为 ,求使
,求使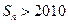 的
的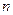 的最小值;
的最小值;
(3)若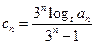 ,证明:
,证明: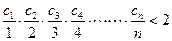 (
(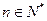 )。
)。
(本小题满分12分)
已知函数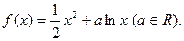
(1)若 上
上 是增函数,求
是增函数,求 的取值范围;
的取值范围;
(2)若 ;
;
(3)若